11 Statistical Model Building
One of the main tools for statistical building multiple regression models is a nested F test. Two models are nested if the parameters in the smaller model are a subset of the parameters in the larger model. AND the two models must contain the exact same observations (be careful of missing values for some variables and not for others!).
\[\begin{eqnarray*} SSR &=& \sum (\hat{Y}_i - \overline{Y})^2 \\ SSE &=& \sum (Y_i - \hat{Y}_i)^2 \\ SSTO &=& \sum (Y_i - \overline{Y})^2 \\ SSTO &=& SSE + SSR \end{eqnarray*}\] Convince yourself that \(SSE(X_1) > SSE(X_1, X_2)\) (where the variables in parentheses indicate which variables are included in the model). It is because the calculus in least squares says that more variables will produce smaller SSE (otherwise \(b_2\) would be estimated to be zero).
Let \[SSR(X_2 | X_1 ) = SSE(X_1) - SSE(X_1, X_2).\] We call \(SSR(X_2 | X_1 )\) the extra sum of squares. It is the marginal reduction in the error sum of squares when one (or more) explanatory variable(s) is added to the model (given that the other explanatory variables are already in the model). Because we know that SSTO does not change for any number of variables (make sure the sample size \(n\) doesn’t change due to missing observations!), we can write SSR in a variety of ways.
\[\begin{eqnarray*}
SSR(X_3| X_1, X_2) &=& SSE(X_1, X_2) - SSE(X_1, X_2, X_3)\\
&=& SSR(X_1, X_2, X_3) - SSR(X_1, X_2)\\
SSR(X_1, X_2 | X_3 ) &=& SSE(X_3) - SSE(X_1, X_2, X_3)\\
&=& SSR(X_1, X_2, X_3) - SSR(X_3)\\
\end{eqnarray*}\]
Consider two nested models:
Model 1: \(E[Y] = \beta_0 + \beta_1 X_1\) \[SSTO = SSR(X_1) + SSE(X_1)\]
Model 2: \(E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2\)
\[\begin{eqnarray*}
SSTO &=& SSR(X_1, X_2) + SSE(X_1, X_2)\\
SSR(X_1, X_2) &=& SSR(X_1) + SSR(X_2 | X_1) \\
SSTO &=& SSR(X_1) + SSR(X_2 | X_1) + SSE(X_1, X_2)\\
\end{eqnarray*}\]
(a) \(SSR(X_1)\) measures the contribution of \(X_1\) alone.
(b) \(SSR(X_2 | X_1)\) measures the contribution of \(X_2\) given \(X_1\) is in the model.
A typical ANOVA table for a model with three explanatory variables will look something like the table below. Note the hierarchical structure to adding variables:
| Source | SS | df | MS |
|---|---|---|---|
| Regression | \(SSR(X_1, X_2, X_3)\) | 3 | \(MSR (X_1, X_2, X_3) = \frac{SSR(X_1, X_2, X_3)}{3}\) |
| \(X_1\) | \(SSR(X_1)\) | 1 | \(MSR(X_1) = \frac{SSR(X_1)}{1}\) |
| \(X_2 | X_1\) | \(SSR(X_2 | X_1)\) | 1 | \(MSR(X_2 | X_1) = \frac{SSR(X_2 | X_1)}{1}\) |
| \(X_3 | X_1, X_2\) | \(SSR(X_3 | X_1, X_2)\) | 1 | \(MSR(X_3 | X_1, X_2) = \frac{SSR(X_3 | X_1, X_2)}{1}\) |
| Error | \(SSE(X_1, X_2, X_3)\) | \(n-4\) | \(MSE(X_1, X_2, X_3) = \frac{SSE(X_1, X_2, X_3)}{n-p}\) |
11.1 Testing Sets of Coefficients
Previously, we have covered both t-tests for \(H_0: \beta_k = 0\) and using the full model F-test to test whether all coefficients are non-significant. In fact, we can also use full and reduced models to compare mean squares to test any nested models. Recall:
1. Fit full model and obtain SSE(full model)
2. Fit reduced model under \(H_0\) to get SSE(reduced)
3. Use \(F^* = \frac{SSE(reduced) - SSE(full)}{df_{reduced} - df_{full}} \div \frac{SSE(full)}{df_{full}}\)
Note 1: Our best estimate of \(\sigma^2\) will come from the MSE on the full model. MSE is an unbiased estimate of \(\sigma^2\), so we will always use it as the denominator in the F test-statistic.
Note 2: The previous F test we learned (\(H_0: \beta_k = 0 \ \ \forall \ \ k \ne 0\)) is the same as above because SSTO = SSE(reduced) for all \(\beta_k=0\), SSR(reduced) = 0. So, when testing if \(\beta_k = 0 \ \ \forall \ \ k \ne 0\): SSE(reduced) - SSE(full) = SSR(full).
Consider testing the following hypotheses
\(H_0: \beta_2 = \beta_3 = 0\)
\(H_a:\) not both zero
Full model: \(E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3\)
Reduced model: \(E[Y] = \beta_0 + \beta_1 X_1\)
\[\begin{eqnarray*}
SSE(full) &=& SSE(X_1, X_2, X_3)\\
SSE(reduced) &=& SSE(X_1)\\
F^* &=& \frac{SSE(X_1) - SSE(X_1, X_2, X_3)}{(n-2) - (n-4)} \div \frac{SSE(X_1, X_2, X_3)}{n-4}\\
&=& \frac{SSR(X_1, X_2, X_3) - SSR(X_1)}{(n-2) - (n-4)} \div \frac{SSE(X_1, X_2, X_3)}{n-4}\\
&=& \frac{SSR(X_2 | X_1) + SSR(X_3 | X_1, X_2)}{2} \div \frac{SSE(X_1, X_2, X_3)}{n-4}\\
&=& \frac{SSR(X_2, X_3 | X_1)}{2} \div \frac{SSE(X_1, X_2, X_3)}{n-4}\\
&=& \frac{MSR(X_2, X_3 | X_1)}{MSE(X_1, X_2, X_3)}
\end{eqnarray*}\]
11.1.1 Examples
- In considering the output below, let’s say that we’d like to test whether both smoking and mother’s age are needed in the model. The full model is: gained, smoke, mage in the model; the reduced model is the model with gained only.
\[\begin{eqnarray*} F &=& \frac{(1485.09 - 1453.37) / (939 - 937)}{1453.37 / 937} = 10.22 \end{eqnarray*}\]
oz_g_lm <- lm(weight ~ gained, data = births14)
oz_ghm_lm <- lm(weight ~ gained + habit + mage, data = births14)
anova(oz_g_lm)## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.4 4.2e-06 ***
## Residuals 939 1485 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(oz_ghm_lm)## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.83 3.4e-06 ***
## habit 1 25 25.3 16.31 5.8e-05 ***
## mage 1 6 6.4 4.14 0.042 *
## Residuals 937 1453 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(oz_g_lm, oz_ghm_lm)## Analysis of Variance Table
##
## Model 1: weight ~ gained
## Model 2: weight ~ gained + habit + mage
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 939 1485
## 2 937 1453 2 31.7 10.2 4.1e-05 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Because our p-value is so low, we reject \(H_0: \beta_2 = \beta_3 = 0\), and we claim that at least one of smoking habit or mother’s age, mage, is needed in the model (possibly both).
One reason to use a nested F-test (in lieu of a t-test), is for example, if you’d like to know whether
termis an important variable in your model (see model 8 way below with the R code). As noted below,termas a factor variable is responsible for 2 separate coefficients. In order to test whethertermis significant, you would fit the model with and withoutterm, and your null hypothesis would be testing \(H_0: \beta_2 = \beta_3 = 0\).Another reason to use a nested F-test is if you want to simultaneously determine if interaction is needed in your model. You might have 4 explanatory variables, and so you’d have \({4\choose2} = 6\) pairwise interactions to consider. You could test all interaction coefficients simultaneously by fitting a model with only additive effects (reduced) and a model with all the interaction effects (full). By nesting them, you don’t need to test each interaction coefficient one at a time.
Let’s say you want to test \(H_0: \beta_1 = \beta_2\). Note the form of your full and reduced models.
\[\begin{eqnarray*} \mbox{full model}:&& E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3\\ \mbox{reduced model}: && E[Y] = \beta_0 + \beta_c (X_1 + X_2) + \beta_3 X_3\\ \end{eqnarray*}\]
Because the reduced model is a specific form of the full model, the two models are nested. We can reformat the data (i.e., add the first two variables), and run the linear model in R. We can get SSE from the full model and from the reduced model and calculate the F statistic by hand.
- Let’s say you want to test \(H_0: \beta_3 = 47\). Again, note the form of your full and reduced models.
\[\begin{eqnarray*} \mbox{full model}:&& E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3\\ \mbox{reduced model}: && E[Y] = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + 47 * X_3\\ \end{eqnarray*}\] We don’t want to find a coefficient for \(X_3\), so we subtract \(47*X_3\) from each Y value: \[\begin{eqnarray*} \mbox{reduced model}: && E[Y - 47* X_3] = \beta_0 + \beta_1 X_1 + \beta_2 X_2\\ \end{eqnarray*}\] Again, the reduced model is a specific form of the full model, the two models are nested. Using the reformatted data, we run linear models on both the full and reduced models and calculate the F statistic by hand.
11.1.2 Coefficient of Partial Determination
Just as \(R^2\) measures the proportion of reduction in the variation of \(Y\) achieved by the set of explanatory variables, a coefficient of partial determination measures the marginal contribution of one X variable (or a set of X variables) when there are already others in the model.
\[\begin{eqnarray*} R^2_{Y 2|1} = \frac{SSE(X_1) - SSE(X_1, X_2)}{SSE(X_1)} = \frac{SSR(X_2|X_1)}{SSE(X_1)} \end{eqnarray*}\]
The coefficient of partial determination measures the marginal contribution of one X variable when all others are already included in the model.
\(R^2_{Y2|1}\) measures the proportionate reduction in “the variation in \(Y\) remaining after \(X_1\) is included in the model” that is gained by also including \(X_2\) in the model.
11.2 Multicollinearity
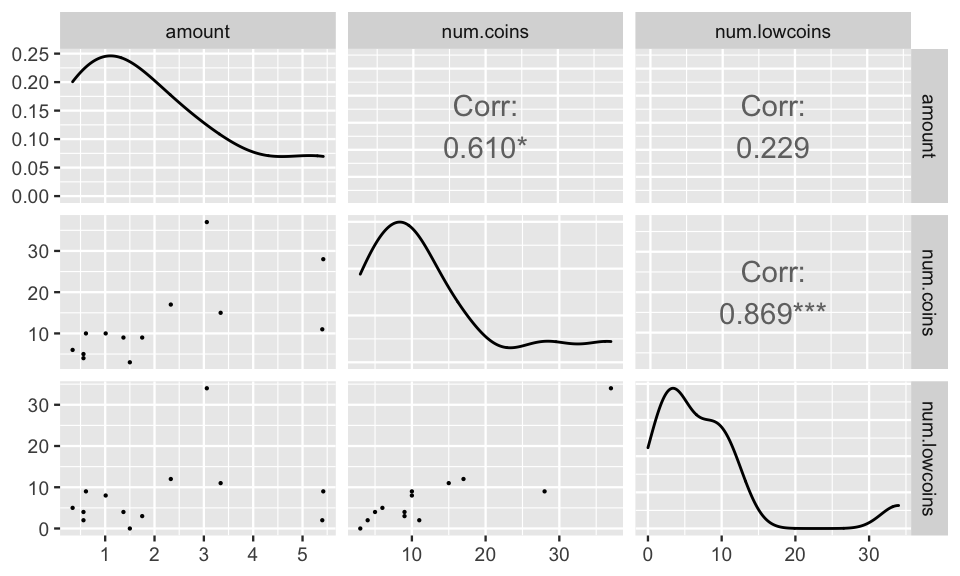
Consider the multiple regression model: \[\begin{eqnarray*} E[Y] &=& \beta_0 + \beta_1 X_1 + \beta_2 X_2\\ Y &=& \mbox{amount of money in pocket}\\ X_1 &=& \# \mbox{ of coins in pocket}\\ X_2 &=& \# \mbox{ of pennies, nickels, dimes in pocket} \end{eqnarray*}\] Using a completely non-random sample, I got the following data:
amount <- c(1.37, 1.01, 1.5, 0.56, 0.61, 3.06, 5.42, 1.75, 5.4, 0.56,
0.34, 2.33, 3.34)
num.coins <- c(9,10,3,5,10,37,28,9,11,4,6,17,15)
num.lowcoins <- c(4,8,0,4,9,34,9,3,2,2,5,12,11)## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.732 0.668 1.10 0.297
## 2 num.coins 0.108 0.0424 2.55 0.0269## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1.73 0.680 2.54 0.0272
## 2 num.lowcoins 0.0462 0.0591 0.781 0.451## # A tibble: 3 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.307 0.466 0.660 0.524
## 2 num.coins 0.296 0.0578 5.13 0.000443
## 3 num.lowcoins -0.246 0.0656 -3.75 0.00376## Analysis of Variance Table
##
## Response: amount
## Df Sum Sq Mean Sq F value Pr(>F)
## num.coins 1 13.64 13.64 14.3 0.0036 **
## num.lowcoins 1 13.48 13.48 14.1 0.0038 **
## Residuals 10 9.57 0.96
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1A few things to notice from the output:
- all 3 of the variables are positively (pairwise correlated).
- the effect of the number of low coins is positive on amount by itself, but negative on amount when the number of coins is in the model.
- the number of low coins is not significant on its own, but it is significant when the number of coins is in the model.
- \(R^2_{Y1} = 63.363/(63.363 + 28.208 + 21.366) = 0.561\)
- \(R^2_{Y2|1} = 28.208 / (28.208 + 21.366) = 0.569\). We see that when number of low coins is added to the model that already contains the number of coins, the SSE is reduced by 56.9%. [ \(SSR(X_1) = 63.363, SSR(X_2|X_1) = 28.208, SSE(X_1, X_2) = 21.366, SSE(X_1) = SSTO - SSR(X_1) = 28.208 + 21.366\) ]
Effects of Multicollinearity
In reality, there is always some degree of correlation between the explanatory variables (pg 283 Kutner et al. (2004)). for regression models, it is important to understand the entire context of the model, particularly for correlated variables.
- Regardless of the degree of multicollinearity, our ability to obtain a good fit and make predictions (mean or individual) is not inhibited.
- If the variables are highly correlated, many different linear combinations of them will produce equally good fits. That is, different samples from the same population may produce wildly different estimated coefficients. For this reason, the variability associated with the coefficients can be quite high. Additionally, the explanatory variables can be statistically not significant even though a definite relationship exists between the response and the set of predictors.
- We can no longer interpret the coefficient to mean “the change in response when this variable increases by one unit and the others are held constant” because it may be impossible to hold the other variables constant. The regression coefficients do not reflect any inherent effect of the particular predictor variable on the response but rather a marginal or partial effect given whatever other correlated predictor variables are included in the model.
- Recall \(SE^2(\underline{b}) = MSE\cdot (X^t X)^{-1}\). If \(X^t X\) has a determinant which is close to zero, taking its inverse is akin to dividing by zero. That is to say, often the SE for the b coefficients can have large sampling variability.
- We will investigate multicollinearity in more depth in Chapter 10 through the Variance Inflation Factor (VIF).
Note: No section ALSM 7.5 or Chapter 8 [Although there is some good stuff in there! Section 7.5 discusses when to standardize your variables – an action that can sometimes be crucially important.]
11.3 Model Selection
We need to come up with something clever to find the model we are going to use. We need to figure out which variables are going to enter into the model, how they are going to appear in the model (transformations, polynomials, interaction terms, etc), and whether we need to also transform our response variable. Why is this such a hard problem?
Suppose we could first agree on a criterion for the “best model”. Maybe we think the best model is that which has the lowest adjusted \(R^2\).
(Recall \(R_a^2=1-\frac{n-1}{n-p}\frac{SSE}{SSTO}\)). Suppose we could also agree on a set of variables that could enter the model, and suppose there are \(m\) of them. How many models do we need to look through?
The smallest model has no predictors in it, i.e. \[E[Y]=\beta_0+\epsilon\]
The largest model has all \(m\) of them in there, i.e. \[E[Y]=\beta_0+\sum_{j=1}^m \beta_jX_j+\epsilon\]
and everything in between.
We can think of this like a tree, we have two choices regarding the first variable, either include it or not, then for each of those, we have two choices for the second, and so forth. There are \(2^m\) possible models we have to look at. Suppose \(m=20\), which isn’t unusual. With 20 variables, there are about 1.05 million different possible models. With 30 variables, there are about 1.07 billion models. Are we going to search through them all? We might if \(m\) is particularly small. \(m=3\) gives 8 possible models, this is quite feasible. Such a search is called all subsets. But otherwise, we need to do something clever.
Algorithm: Best subset selection (from ISLR)
- Let \(M_0\) denote the null model, which contains no predictors. The null model predicts the sample mean of the response variable for each observation.
- For \(k = 1, 2, \ldots m\):
- Fit all \({m\choose k}\) models that contain exactly \(k\) predictors (explanatory variables).
- Pick the best among the \({m\choose k}\) models, and call it \(M_k\). Here best7 is defined as having the smallest SSE, or equivalently, largest \(R^2\).
- Fit all \({m\choose k}\) models that contain exactly \(k\) predictors (explanatory variables).
- Select a single best model from among \(M_0, \ldots ,M_{m}\) using cross-validated prediction error, \(C_p\), AIC, BIC, or adjusted \(R^2\).
11.3.1 Forward Selection
We start with an empty model and add the best available variable at each iteration, checking for needed transformations. (We should also look at interactions which we might suspect. However, looking at all possible interactions (if only 2-way interactions, we could also consider 3-way interactions etc.), things can get out of hand quickly.) Generally for forward selection:
1. We start with the response variable versus all variables and find the best predictor. If there are too many, we might just look at the correlation matrix. However, we may miss out of variables that are good predictors but aren’t linearly related. Therefore, if its possible, a scatter plot matrix would be best.
2. We locate the best variable, and regress the response variable on it.
3. If the variable seems to be useful, we keep it and move on to looking for a second.
4. If not, we stop.
Algorithm: Forward stepwise subset selection (from ISLR)
- Let \(M_0\) denote the null model, which contains no predictors. The null model predicts the sample mean of the response variable for each observation.
- For \(k = 0, 1, \ldots m-1\):
- Consider all \(m - k\) models that augment the predictors in \(M_k\) with one additional predictor.
- Choose the best among these \(m - k\) models, and call it \(M_{k+1}\). Here best is defined as having smallest SSE or highest \(R^2\).
- Consider all \(m - k\) models that augment the predictors in \(M_k\) with one additional predictor.
- Select a single best model from among \(M_0, \ldots ,M_{m}\) using cross-validated prediction error, \(C_p\), AIC, BIC, or adjusted \(R^2\).
Algorithm: Forward selection with F tests
- Let \(M_0\) denote the null model, which contains no predictors. The null model predicts the sample mean of the response variable for each observation.
- Let \(k = 0\):
- Consider all \(m - k\) models that augment the predictors in \(M_k\) with one additional predictor.
- Choose the best among these \(m - k\) models, and call it \(M_{k+1}\). Here best is defined as having the smallest p-value for including the \((k+1)^{th}\) variable given the \(k\) variables are already in the model.
- If the p-value from step b. is less than \(\alpha_e\), consider \(M_{k+1}\) and augment \(k\) by 1. Go back to step a. If the p-value from step b. is larger than \(\alpha_e\), report model \(M_k\) and stop the algorithm.
- Consider all \(m - k\) models that augment the predictors in \(M_k\) with one additional predictor.
It is doing exactly what we want, right???
Suppose that you have to take an exam that covers 100 different topics, and you do not know any of them. The rules, however, state that you can bring two classmates as consultants. Suppose also that you know which topics each of your classmates is familiar with. If you could bring only one consultant, it is easy to figure out who you would bring: it would be the one who knows the most topics (the variable most associated with the answer). Let’s say this is Kelly who knows 85 topics.
With two consultants you might choose Kelly first, and for the second option, it seems reasonable to choose the second most knowledgeable classmate (the second most highly associated variable), for example Jamie, who knows 75 topics. The problem with this strategy is that it may be that the 75 subjects Jamie knows are already included in the 85 that Kelly knows, and therefore, Jamie does not provide any knowledge beyond that of Kelly.
A better strategy is to select the second not by considering what he or she knows regarding the entire agenda, but by looking for the person who knows more about the topics than the first does not know (the variable that best explains the residual of the equation with the variables entered). It may even happen that the best pair of consultants are not the most knowledgeable, as there may be two that complement each other perfectly in such a way that one knows 55 topics and the other knows the remaining 45, while the most knowledgeable does not complement anybody.8
Consider people A, B, C, D who know the following topics:
A: {1, 2, 3, 4, 5, 6, 7}
B: {8, 9, 10}
C: {1, 2, 3, 4, 8, 10}
D: {5, 6, 7, 9, 11}
Forward, choose A and then B (and you'd know topics 1-10).
Backward (& best subsets), choose C and D (and you'd know topics 1-11).Forward Stepwise Selection using F-tests
This method follows in the same way as Forward Regression, but as each new variable enters the model, we check to see if any of the variables already in the model can now be removed. This is done by specifying two values, \(\alpha_e\) as the \(\alpha\) level needed to enter the model, and \(\alpha_l\) as the \(\alpha\) level needed to leave the model. We require that \(\alpha_e<\alpha_l\), otherwise, our algorithm could cycle, we add a variable, then immediately decide to delete it, continuing ad infinitum. This is bad.
- We start with the empty model, and add the best predictor, assuming the p-value associated with it is smaller than \(\alpha_e\).
- Now, we find the best of the remaining variables, and add it if the p-value is smaller than \(\alpha_e\). If we add it, we also check to see if the first variable can be dropped, by calculating the p-value associated with it (which is different from the first time, because now there are two variables in the model). If its p-value is greater than \(\alpha_l\), we remove the variable.
- We continue with this process until there are no more variables that meet either requirements. In many situations, this will help us from stopping at a less than desirable model.
How do you choose the \(\alpha\) values? If you set \(\alpha_e\) to be very small, you might walk away with no variables in your model, or at least not many. If you set it to be large, you will wander around for a while, which is a good thing, because you will explore more models, but you may end up with variables in your model that aren’t necessary.
11.3.2 Backward Selection
- Start with the full model including every term (and possibly every interaction, etc.).
- Remove the variable that is least significant (biggest p-value) in the model.
- Continue removing variables until all variables are significant at the chosen \(\alpha\) level.
Algorithm: Backward stepwise selection (from ISLR)
- Let \(M_{full}\) denote the full model, which contains all \(m\) predictors.
- For \(k = m, m-1, \ldots, 1\):
- Consider all k models that contain all but one of the predictors in \(M_k\) (including a total of \(k - 1\) predictors).
- Choose the best among these \(k\) models, and call it \(M_{k-1}\). Here best is defined as having the smallest SSE or highest \(R^2\).
- Consider all k models that contain all but one of the predictors in \(M_k\) (including a total of \(k - 1\) predictors).
- Select a single best model from among \(M_0, \ldots ,M_{m}\) using cross-validated prediction error, \(C_p\), AIC, BIC, or adjusted \(R^2\).
Algorithm: Backward selection with F tests
- Let \(M_{full}\) denote the full model, which contains all \(m\) predictors.
- Let \(k = m\):
- Consider all k models that contain all but one of the predictors in \(M_k\) (including a total of \(k - 1\) predictors).
- Choose the best among these \(k\) models, and call it \(M_{k-1}\). Here best is defined as removing the largest p-value for including the \((k)^{th}\) variable given the \(k-1\) variables are already in the model.
- If the p-value from step b. is larger than \(\alpha_r\), consider \(M_{k}\) and decrease \(k\) by 1. Go back to step a. If the p-value from step b. is smaller than \(\alpha_r\), report model \(M_k\) and stop the algorithm.
- Consider all k models that contain all but one of the predictors in \(M_k\) (including a total of \(k - 1\) predictors).
Do any of the above methods represent a fool-proof strategy for fitting a model? No, but they are a start. Remember, it is important to always check the residuals and logical interpretation of the model.
11.4 Other ways for comparing models
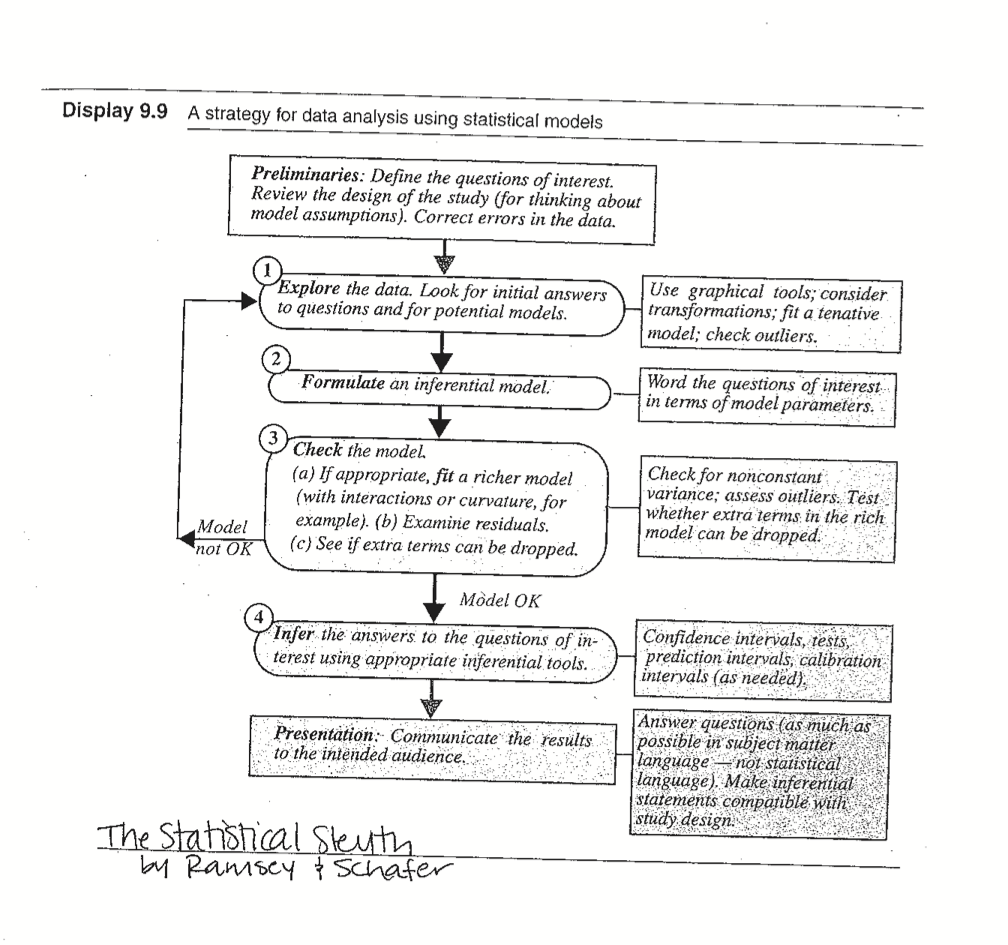
Figure 6.4: A strategy for data analysis using statistical models. Source: Ramsey and Schafer (2012)
11.4.1 Analysis of Appropriateness of Model
Scatter Plot Matrix
Plots all variables against all others. Gives indications of need to consider transformations of predictors. Also shows predictors that are highly correlated with other predictors, thus possibly not needing to be included in the model.
Correlation Matrix
A numerical version of the scatterplot matrix, the correlation matrix computes the correlations between groups of variables. We want predictor variables that are highly correlated with the response, but we need to be careful about predictor variables that are highly correlated with each other.
Residual Plot
Plots fitted values against residuals. As before, we should see no trend and constant variance.
Residuals should also be plotted against variables individually, including variables that were left out of the model, as well as possible interactions.
If there are trends in the residual plots against the variables in the model, you might consider a transformation or adding a polynomial term. If there are trends in the residual plots against variables left out of the model, you might consider adding those variables to the model. If there are trends in the residual plot against interaction terms (like \(X_1X_2\)), then you might consider adding that interaction term to the model.
11.5 Getting the Variables Right
In terms of selecting the variables to model a particular response, four things can happen:
- The regression model is correct!
- The regression model is underspecified.
- The regression model contains extraneous variables.
- The regression model is overspecified.
Underspecified
A regression model is underspecified if it is missing one or more important predictor variables. Being underspecified is the worst case scenario because the model ends up being biased and predictions are wrong for virtually every observation. Additionally, the estimate of MSE tends to be big which yields larger confidence intervals for the estimates (less chance for significance).
Consider another SAT dataset. We see that if we don’t stratify by the fraction of students in the state who took the SAT (0-22%, 22-49%, 49-81%). So much changes! The slopes are negative in the large group and positive in the subgroups. Additionally, the \(R^2\) value goes from 0.193 to 0.806!! The model without the fraction of students is underspecified and quite biased. It doesn’t matter how many observations we collect, the model will always be wrong. Underspecifying the model is the worst of the possible things that can happen.
library(mosaic)
library(mosaicData)
SAT <- SAT %>%
mutate(SAT, frac_group = cut(frac, breaks=c(0, 22, 49, 81),
labels=c("low fraction",
"medium fraction",
"high fraction")))
SAT %>%
ggplot(aes(x = salary, y = sat)) +
geom_point(aes(shape = frac_group, color = frac_group)) +
geom_smooth(method = "lm", se = FALSE)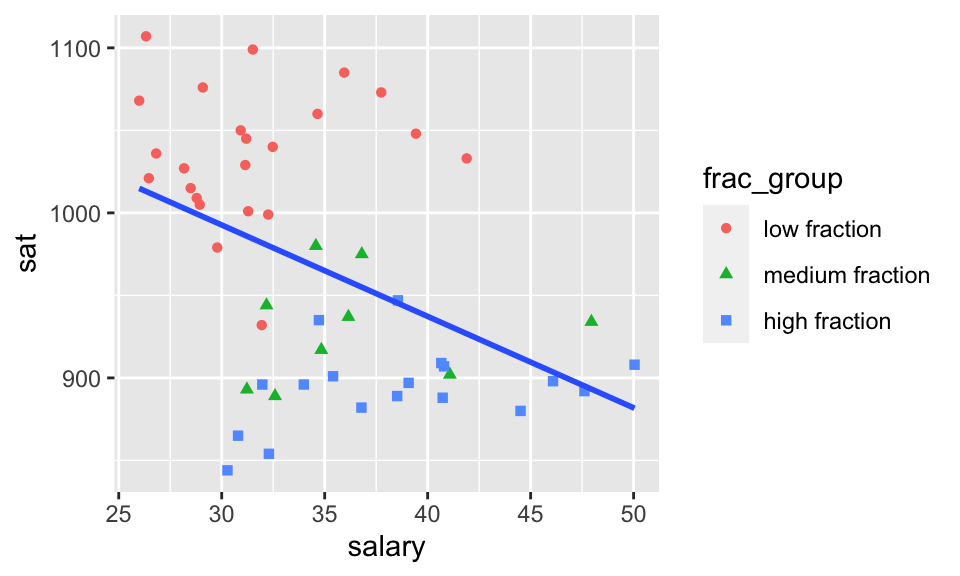
SAT %>%
ggplot(aes(x = salary, y = sat, group = frac_group, color = frac_group)) +
geom_point(aes(shape = frac_group)) +
geom_smooth(method = "lm", se = FALSE, fullrange = TRUE)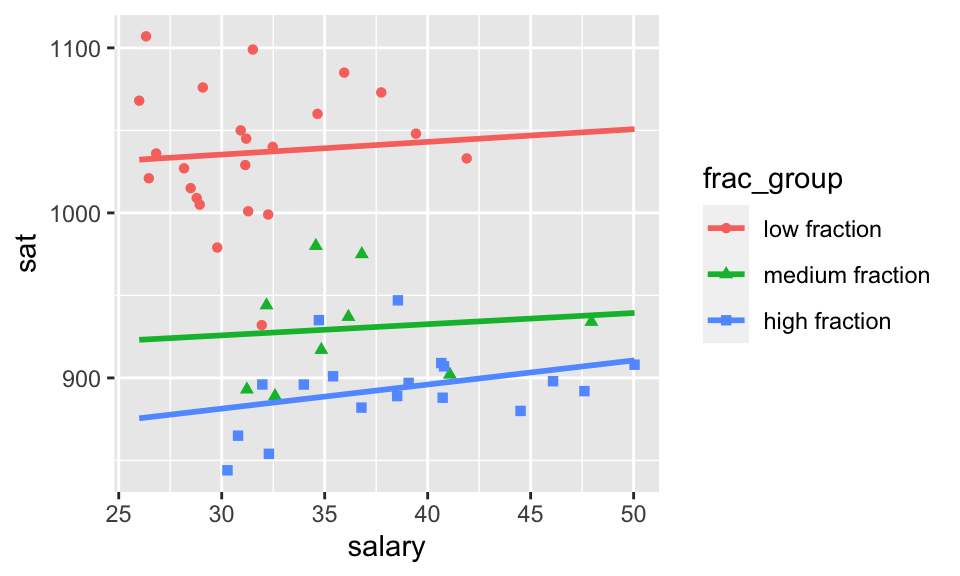
Extraneous
The third type of variable situation comes when extra variables are included in the model but the variables are neither related to the response nor are they correlated with the other explanatory variables. Generally, extraneous variables are not so problematic because they produce models with unbiased coefficient estimators, unbiased predictions, and unbiased MSE. The worst thing that happens is that the error degrees of freedom is lowered which makes confidence intervals wider and p-values bigger (lower power). Also problematic is that the model becomes unnecessarily complicated and harder to interpret.
Overspecified
When a model is overspecified, there are one or more redundant variables. That is, the variables contain the same information as other variables (i.e., are correlated!). As we’ve seen, correlated variables cause trouble because they inflate the variance of the coefficient estimates. With correlated variables it is still possible to get unbiased prediction estimates, but the coefficients themselves are so variable that they cannot be interpreted (nor can inference be easily performed).
Generally: the idea is to use a model building strategy with some criteria (F-tests, AIC, BIC, Adjusted \(R^2\), \(C_p\), LASSO, Ridge regression) to find the middle ground between an underspecified model and an overspecified model.
11.6 A Model Building Strategy9
Model building is definitely an art. Unsurprisingly, there are many approaches to model building, but here is one strategy, consisting of seven steps, that is commonly used when building a regression model.
The first step
Decide on the type of model that is needed in order to achieve the goals of the study. In general, there are five reasons one might want to build a regression model. They are:
- For predictive reasons - that is, the model will be used to predict the response variable from a chosen set of predictors.
- For theoretical reasons - that is, the researcher wants to estimate a model based on a known theoretical relationship between the response and predictors.
- For control purposes - that is, the model will be used to control a response variable by manipulating the values of the predictor variables.
- For inferential reasons - that is, the model will be used to explore the strength of the relationships between the response and the predictors.
- For data summary reasons - that is, the model will be used merely as a way to summarize a large set of data by a single equation.
The second step
Decide which explanatory variables and response variable on which to collect the data. Collect the data.
The third step
Explore the data. That is:
- On a univariate basis, check for outliers, gross data errors, and missing values.
- Study bivariate relationships to reveal other outliers, to suggest possible transformations, and to identify possible multicollinearities.
I can’t possibly over-emphasize the data exploration step. There’s not a data analyst out there who hasn’t made the mistake of skipping this step and later regretting it when a data point was found in error, thereby nullifying hours of work.
The fourth step
(The fourth step is very good modeling practice. It gives you a sense of whether or not you’ve overfit the model in the building process.) Randomly divide the data into a training set and a validation set:
- The training set, with at least 15-20 error degrees of freedom, is used to estimate the model.
- The validation set is used for cross-validation of the fitted model.
The fifth step
Using the training set, identify several candidate models:
- Use best subsets regression.
- Use all subsets, stepwise, forward, or backward selection regression. Using different alpha-to-remove and alpha-to-enter values can lead to a variety of models.
The sixth step
Select and evaluate a few “good” models:
- Select the models based on the criteria we learned, as well as the number and nature of the predictors.
- Evaluate the selected models for violation of the model conditions.
- If none of the models provide a satisfactory fit, try something else, such as collecting more data, identifying different predictors, or formulating a different type of model.
The seventh and final step
Select the final model:
- A small mean square prediction error (or larger cross-validation \(R^2\)) on the validation data is a good predictive model (for your population of interest).
- Consider residual plots, outliers, parsimony, relevance, and ease of measurement of predictors.
And, most of all, don’t forget that there is not necessarily only one good model for a given set of data. There might be a few equally satisfactory models.
11.6.1 Thoughts on Model Selection…
Question: Did females receive lower starting salaries than males?10
model:
y: log(salary)
x’s: seniority, age, experience, education, sex
In Ramsey and Schafer (2012), they first find a good model using only seniority, age, experience, and education (including considerations of interactions/quadratics). Once they find a suitable model (Model 1), they then add the sex variable to this model to determine if it is significant. (H0: Model 1 vs HA: Model 1 + sex) In other regression texts, the models considered would include the sex variable from the beginning, and work from there, but always keeping the sex variable in. What are the pluses/minuses of these approaches?
Response It seems possible, and even likely, that sex would be associated with some of these other variables, so depending on how the model selection that starts with sex included was done, it would be entirely possible to choose a model that includes sex but not one or more of the other variables, and in which sex is significant. If however, those other variables were included, sex might not explain a significant amount of variation beyond those others. Whereas the model selection that doesn’t start with sex would be more likely to include those associated covariates to start with.
One nice aspect of both methods is that they both end up with sex in the model; one difficulty is when a model selection procedure ends up removing the variable of interest and people then claim that the variable of interest doesn’t matter. However, it is often advantageous to avoid model selection as much as possible. Each model answers a different question, and so ideally it would be good to decide ahead of time what the question of interest is.
In this case there are two questions of interest; are there differences at all (univariate model on sex), and are there differences after accounting for the covariates (multivariate model)? If the differences get smaller after adjusting for the covariates, then that leads to the very interesting question of why that is, and whether those differences are also part of the sex discrimination. Consider the explanation that the wage gap between men and women is due to men in higher-paying jobs, when really, that’s part of the problem, that jobs that have more women in them pay less. :( The point, though, is that one model may not be sufficient for a particular situation, and looking for one “best” model can be misleading.
11.7 Reflection Questions
11.7.1 Decomposing sums of squares
- How do SSE, SSR, and SSTO change when variables are added to the model?
- What does \(SSR(X_2 | X_1)\) really mean? How is it defined?
- How do we break up SSR in the ANOVA table? Note: the order of variables maters!
- How do you tests sets of coefficients that aren’t in the right order? Or that equal a constant? Or that equal each other?
- If you are doing a nested F-test without
anova()output, how do you find the \(F^*\) critical value? (Hint: useqf()in R)
11.7.2 Multicollinearity
- What does multicollinearity mean?
- What are the effects of multicollinearity on various aspects of regression analyses?
- What are the effects of correlated predictors on various aspects of regression analyses?
- (More in ALSM chapter 10: variance inflation factors, and how to use them to help detect multicollinearity)
- How can multicollinearity problems be reduced in the analysis?
- What are the big regression pitfalls? (including extrapolation, non-constant variance, autocorrelation (e.g., time series), overfitting, excluding important predictor variables, missing data, and power and sample size.)
11.7.3 Building models
- What is the impact of the four different kinds of models with respect to their “correctness”: correctly specified, underspecified, overspecified, and correct but with extraneous predictors?
- How do you conduct stepwise regression “by hand” (using either F tests or one of the other criteria)?
- What are the limitations of stepwise regression?
- How can you choose an optimal model based on the \(R^2\) value, \(R^2_{adj}\), MSE, AIC, BIC, or \(C_p\) criterion?
- What are the seven steps of good model building strategy?
11.8 Ethics Considerations
Consider the following example on Building Compassion into Your Modelling Variables by Heather Krause at We All Count.
The example describes a hypothetical budget app whose goal is to help the user save money. The explanatory variable is whether or not the app is used; the response variable is the amount of money saved.
Heather suggests that there are three strategies to model the variables of interest and that each of the three strategies privilege different groups of people. In all three strategies, we randomly assign the budgeting app to the individuals in the study in order to determine a causal mechanism between the budgeting app and the amount of money saved.
Of additional interest is the variable which describes the proportion of an individual’s income which is disposable income (the amount left over after paying for food, shelter, heat, etc.).
The key to the blog is not to define the technical details of how to work with different types of variables (confounder, moderator, or mediator). The point of the blog is to recognize that there are different ways to model covariates, and how you model them will change who the results privilege.
Strategy 1: fix disposable income proportion (confounder)
In the first strategy you include the proportion of disposable income of the individuals in the model as a covariate. Here, the interpretation of the budgeting app coefficient is given as “while all other variables are constant.” The model can be something as straightforward as a linear model,
But maybe that doesn’t make sense because the whole point of the app is that it will change the proportion of disposable income, which in turn affects the amount of savings.
Using the example in the blog, if we:
isolate the effect that the budgeting app is having regardless of what portion of their income is disposable. I run this model and it turns out that their app isn’t having much of an effect at all on whether or not people saved at least $175 extra dollars. Sorry guys, I say in the meeting.
Strategy 2: disposable income proportion interacting (moderator)
If the amount of disposable income changes the impact of the budgeting app on the amount of money saved, we say that disposable income and the budgeting app interact. That is, if you are reasonably flush, maybe the app can really help you save a lot of money. If your finances are already very tight, you probably aren’t spending a lot of money on non-essentials. So the budgeting app may not help at all for those with low disposable income proportion.
If you use this model, you are assuming that the success of the app depends entirely on whether or not you can adjust your disposable income, giving voice to people across the spectrum of that experience, both positive and negative. That’s really important if you care about helping people already budgeted to within an inch of their life.
Sure your app might be a prettier, faster way to do that, but it might not be worth the 175 dollars to someone who is counting all of theirs.
Strategy 3: disposable income proportion as a mediator
A mediator variable is one which is on the causal pathway from \(X\) to \(Y\). The modeling strategy involves causal inference, possibly modeling with a directed acyclic graph (DAG). Alternatively, first model whether \(X\) predicts the mediator and whether the mediator predicts \(Y\) (Baron and Kenny 1986). Lots more information here.
This model shows how the app performs assuming you are in a position to adjust expenses, that is the expected mechanism of change. If you say “the app works” based on this model you are privileging those in a position to benefit from how it works. Which in this case is people who have the financial leeway to do so.
11.9 R: ANOVA decompisition - tips
We return to the tips data which was used in Section 9.611.
Is this the best model to explain variation in tips?
Note: when a single dataset is used to build and fit the model, we penalize the fitting (think \(R^2_{adj}\)). When different data are used, i.e., with CV, there is no need to use a metric with penalization.
11.9.1 Analysis of variance (ANOVA)
-
Main Idea: Decompose the total variation on the outcome into:
the variation that can be explained by the each of the variables in the model
the variation that can’t be explained by the model (left in the residuals)
- If the variation that can be explained by the variables in the model is greater than the variation in the residuals, this signals that the model might be “valuable” (at least one of the \(\beta\)s not equal to 0)
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| Party | 1 | 1189 | 1188.64 | 285.71 | 0.00 |
| Age | 2 | 38 | 19.01 | 4.57 | 0.01 |
| Residuals | 165 | 686 | 4.16 | NA | NA |
ANOVA output, with totals
| term | df | sumsq | meansq | statistic | p.value |
|---|---|---|---|---|---|
| Party | 1 | 1189 | 1188.64 | 285.71 | 0 |
| Age | 2 | 38 | 19.01 | 4.57 | 0.01 |
| Residuals | 165 | 686 | 4.16 | ||
| Total | 168 | 1913 |
Sum of squares
| term | df | sumsq |
|---|---|---|
| Party | 1 | 1189 |
| Age | 2 | 38 |
| Residuals | 165 | 686 |
| Total | 168 | 1913 |
- \(SS_{Total}\): Total sum of squares, variability of outcome, \(\sum_{i = 1}^n (y_i - \bar{y})^2\)
- \(SS_{Error}\): Residual sum of squares, variability of residuals, \(\sum_{i = 1}^n (y_i - \hat{y})^2\)
- \(SS_{Model} = SS_{Total} - SS_{Error}\): Variability explained by the model
11.10 R: nested F test - births
Every year, the US releases to the public a large data set containing information on births recorded in the country. This data set has been of interest to medical researchers who are studying the relation between habits and practices of expectant mothers and the birth of their children. This is a random sample of 1,000 cases from the data set released in 2014. Data description here.
library(openintro)
data(births14)
births14 <- births14 %>%
select(-fage, -visits) %>%
drop_na() %>%
mutate(term = case_when(
weeks <= 38 ~ "early",
weeks <= 40 ~ "full",
TRUE ~ "late"
))
names(births14)## [1] "mage" "mature" "weeks" "premie"
## [5] "gained" "weight" "lowbirthweight" "sex"
## [9] "habit" "marital" "whitemom" "term"Notice that the variable names we’ll use are mage, weight, gained, and habit.
- Interested is in predicting a baby’s
weightfrom the pounds a mothergained.
## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.83 0.0912 74.9 0
## 2 gained 0.0124 0.00267 4.63 0.00000423## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.4 4.2e-06 ***
## Residuals 939 1485 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- What if smoking
habitis included as a variable?
## # A tibble: 3 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.91 0.0924 74.8 0
## 2 gained 0.0119 0.00266 4.49 0.00000813
## 3 habitsmoker -0.507 0.126 -4.03 0.0000598## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.8 3.5e-06 ***
## habit 1 25 25.3 16.3 6.0e-05 ***
## Residuals 938 1460 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- What if smoking
habitand weightgainedinteract?
## # A tibble: 4 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.89 0.0978 70.5 0
## 2 gained 0.0124 0.00285 4.35 0.0000153
## 3 habitsmoker -0.400 0.259 -1.55 0.123
## 4 gained:habitsmoker -0.00368 0.00782 -0.471 0.638## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.74 3.6e-06 ***
## habit 1 25 25.3 16.24 6.0e-05 ***
## gained:habit 1 0 0.3 0.22 0.64
## Residuals 937 1459 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- What happens to the model if another quantitative variable, the mother’s age
mage, is added?
## # A tibble: 4 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.49 0.225 28.8 2.94e-131
## 2 gained 0.0122 0.00265 4.59 5.11e- 6
## 3 habitsmoker -0.494 0.126 -3.93 9.07e- 5
## 4 mage 0.0144 0.00707 2.03 4.22e- 2## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.83 3.4e-06 ***
## habit 1 25 25.3 16.31 5.8e-05 ***
## mage 1 6 6.4 4.14 0.042 *
## Residuals 937 1453 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- What happens to the model if another quantitative variable is added with the interaction?
## # A tibble: 5 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 6.48 0.227 28.5 2.27e-129
## 2 gained 0.0126 0.00285 4.43 1.07e- 5
## 3 habitsmoker -0.397 0.259 -1.54 1.25e- 1
## 4 mage 0.0143 0.00707 2.02 4.33e- 2
## 5 gained:habitsmoker -0.00335 0.00781 -0.430 6.68e- 1## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.81 3.4e-06 ***
## habit 1 25 25.3 16.30 5.9e-05 ***
## mage 1 6 6.4 4.13 0.042 *
## gained:habit 1 0 0.3 0.18 0.668
## Residuals 936 1453 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- What is the F-test to see if
mageshould be added to the model with interaction? (borderline, the p-value onmageis 0.0423 for \(H_0: \beta_{mage}=0\))
anova(oz_gih_lm, oz_gihm_lm)## Analysis of Variance Table
##
## Model 1: weight ~ gained * habit
## Model 2: weight ~ gained * habit + mage
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 937 1459
## 2 936 1453 1 6.36 4.09 0.043 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- Can both the interaction and
magebe dropped? (Yes, the p-value is reasonably large indicating that there is no evidence that either of the coefficients is different from zero. Now the test is \(H_0: \beta_{gainxsmk} = \beta_{mage} = 0\).)
anova(oz_gh_lm, oz_gihm_lm)## Analysis of Variance Table
##
## Model 1: weight ~ gained + habit
## Model 2: weight ~ gained * habit + mage
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 938 1460
## 2 936 1453 2 6.7 2.16 0.12- Calculate the coefficient of partial determination for
magegivengainedandhabit.
anova(oz_ghm_lm)## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 21.83 3.4e-06 ***
## habit 1 25 25.3 16.31 5.8e-05 ***
## mage 1 6 6.4 4.14 0.042 *
## Residuals 937 1453 1.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
6.42 / (6.42 + 1453.37)## [1] 0.0044The variability (in ounces of baby weight) remaining after modeling with gained and habit is reduced by a further 0.4% when additionally adding mage.
- What happens if variables are entered into the model in a different order?
## # A tibble: 3 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 7.08 0.245 28.9 4.87e-132
## 2 maritalnot married -0.199 0.0926 -2.15 3.22e- 2
## 3 mage 0.00725 0.00787 0.920 3.58e- 1## # A tibble: 3 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 7.08 0.245 28.9 4.87e-132
## 2 mage 0.00725 0.00787 0.920 3.58e- 1
## 3 maritalnot married -0.199 0.0926 -2.15 3.22e- 2## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## marital 1 12 12.33 7.69 0.0057 **
## mage 1 1 1.36 0.85 0.3576
## Residuals 938 1505 1.60
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## mage 1 6 6.31 3.93 0.048 *
## marital 1 7 7.38 4.60 0.032 *
## Residuals 938 1505 1.60
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1- On a different note… the variable
termhas three levels (“early”, “full”, and “late”). Notice how the variable itself can be in the model or out of the model but that when it is in the model it uses two degrees of freedom because there are two coefficients to estimate. Whenterminteracts withgainedthere are an additional two coefficients to estimate (both of the interaction coefficients in the model).
oz_gtm_lm <- lm(weight ~ gained + term + mage, data=births14)
oz_gitm_lm <- lm(weight ~ gained * term + mage, data=births14)
tidy(oz_gtm_lm)## # A tibble: 5 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 5.72 0.213 26.9 2.32e-118
## 2 gained 0.0109 0.00246 4.44 9.93e- 6
## 3 termfull 1.02 0.0833 12.3 3.99e- 32
## 4 termlate 1.07 0.113 9.49 1.85e- 20
## 5 mage 0.0171 0.00654 2.61 9.08e- 3
anova(oz_gtm_lm)## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 25.40 5.6e-07 ***
## term 2 228 114.2 85.67 < 2e-16 ***
## mage 1 9 9.1 6.84 0.0091 **
## Residuals 936 1248 1.3
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
tidy(oz_gitm_lm)## # A tibble: 7 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 5.77 0.236 24.5 1.26e-102
## 2 gained 0.00929 0.00430 2.16 3.11e- 2
## 3 termfull 0.911 0.187 4.88 1.28e- 6
## 4 termlate 1.09 0.247 4.42 1.08e- 5
## 5 mage 0.0171 0.00655 2.61 9.27e- 3
## 6 gained:termfull 0.00365 0.00559 0.652 5.14e- 1
## 7 gained:termlate -0.000469 0.00703 -0.0667 9.47e- 1
anova(oz_gitm_lm)## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## gained 1 34 33.9 25.37 5.7e-07 ***
## term 2 228 114.2 85.54 < 2e-16 ***
## mage 1 9 9.1 6.83 0.0091 **
## gained:term 2 1 0.4 0.30 0.7388
## Residuals 934 1247 1.3
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 111.11 R: model building - SAT scores
These notes belong at the end… I’m putting them here to highlight them before the full analysis.
- Notice that \(C_p\) and F-tests use a “full” model MSE. Typically, the MSE will only be an unbiased predictor of \(\sigma^2\) in backwards variable selection.
- BIC usually results in fewer parameters in the model than AIC.
- Using different selection criteria may lead to different models (there is no one best model).
- The order in which variables are entered does not necessarily represent their importance. As a variable entered early on can be dropped at a later stage because it is predicted well from the other explanatory variables that have been subsequently added to the model.
Consider the multiple regression model: \[\begin{eqnarray*} E[Y] &=& \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \beta_4 X_4 + \beta_5 X_5 + \beta_6 X_6\\ Y &=& \mbox{state ave SAT score}\\ X_1 &=& \% \mbox{ of eligible seniors who took the exam, } takers\\ X_2 &=& \mbox{median income of families of test takers, } income\\ X_3 &=& \mbox{ave number of years of formal eduction, } years\\ X_4 &=& \% \mbox{ of test takers who attend public school, } public\\ X_5 &=& \mbox{total state expenditure on public secondary schools (\$100 /student), } expend \\ X_6 &=& \mbox{median percentile rank of test takers within their secondary school class, } rank \end{eqnarray*}\]
sat_data <- read_csv("http://pages.pomona.edu/~jsh04747/courses/math158/sat.csv") %>%
mutate(ltakers = log(takers))
sat_n <- nrow(sat_data) # always be wary of missing rows, though!AIC and BIC in R
- The model with no variables
## # A tibble: 1 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 948. 10.2 92.9 7.89e-56
lm(sat ~ 1, data = sat_data) %>% glance() %>%
mutate(mse = sigma^2, sse = mse*df.residual) %>%
select(mse, sse, AIC, BIC, df.residual, nobs)## # A tibble: 1 × 6
## mse sse AIC BIC df.residual nobs
## <dbl> <dbl> <dbl> <dbl> <int> <int>
## 1 5112. 245376. 560. 564. 48 49- The model on
ltakers
## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1112. 12.4 89.8 3.11e-54
## 2 ltakers -59.2 4.17 -14.2 1.27e-18
lm(sat ~ ltakers, data = sat_data) %>% glance() %>%
mutate(mse = sigma^2, sse = mse*df.residual) %>%
select(mse, sse, AIC, BIC, df.residual, nobs)## # A tibble: 1 × 6
## mse sse AIC BIC df.residual nobs
## <dbl> <dbl> <dbl> <dbl> <int> <int>
## 1 987. 46369. 481. 487. 47 49Best possible subsets
Note that the outcome is the best model with one variable, the best model with two variables, etc. Therefore, the selection is based on SSE only. It is your job as the analyst to differentiate between the models of different sizes. You could use \(R_{adj}^2\), AIC, BIC, etc. Here is seems like the 4 variable model is a good contender for best model.
best_lms<- leaps::regsubsets(sat ~ ltakers + income + years + public + expend + rank,
data=sat_data, nvmax = 6)## # A tibble: 6 × 11
## `(Intercept)` ltakers income years public expend rank r.squared adj.r.squared
## <lgl> <lgl> <lgl> <lgl> <lgl> <lgl> <lgl> <dbl> <dbl>
## 1 TRUE TRUE FALSE FALSE FALSE FALSE FALSE 0.811 0.807
## 2 TRUE TRUE FALSE FALSE FALSE TRUE FALSE 0.895 0.890
## 3 TRUE TRUE FALSE TRUE FALSE TRUE FALSE 0.900 0.893
## 4 TRUE TRUE FALSE TRUE FALSE TRUE TRUE 0.911 0.903
## 5 TRUE TRUE TRUE TRUE FALSE TRUE TRUE 0.913 0.903
## 6 TRUE TRUE TRUE TRUE TRUE TRUE TRUE 0.913 0.900
## # … with 2 more variables: BIC <dbl>, mallows_cp <dbl>Forward Variable Selection: F-tests
add1(lm(sat ~ 1, data = sat_data), sat ~ ltakers + income + years +
public + expend + rank, test = "F")## Single term additions
##
## Model:
## sat ~ 1
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 245376 419
## ltakers 1 199007 46369 340 201.71 < 2e-16 ***
## income 1 102026 143350 395 33.45 5.7e-07 ***
## years 1 26338 219038 416 5.65 0.022 *
## public 1 1232 244144 421 0.24 0.629
## expend 1 386 244991 421 0.07 0.787
## rank 1 190297 55079 348 162.38 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
add1(lm(sat ~ ltakers, data = sat_data), sat ~ ltakers + income + years +
public + expend + rank, test = "F")## Single term additions
##
## Model:
## sat ~ ltakers
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 46369 340
## income 1 785 45584 341 0.79 0.3781
## years 1 6364 40006 335 7.32 0.0095 **
## public 1 449 45920 341 0.45 0.5058
## expend 1 20523 25846 313 36.53 2.5e-07 ***
## rank 1 871 45498 341 0.88 0.3529
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
add1(lm(sat ~ ltakers + expend, data = sat_data), sat ~ ltakers + income + years +
public + expend + rank, test = "F")## Single term additions
##
## Model:
## sat ~ ltakers + expend
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 25846 313
## income 1 53 25792 315 0.09 0.76
## years 1 1248 24598 313 2.28 0.14
## public 1 1 25845 315 0.00 0.96
## rank 1 1054 24792 313 1.91 0.17Note: Sum of Sq refers to the SSR(new variable \(|\) current model) (additional reduction in SSE). RSS is the SSE for the model that contains the current variables and the new variable.
Backward Variable Selection: F-tests
# all the variables
drop1(lm(sat ~ ltakers + income + years + public + expend + rank,
data=sat_data), test="F")## Single term deletions
##
## Model:
## sat ~ ltakers + income + years + public + expend + rank
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 21397 312
## ltakers 1 2150 23547 315 4.22 0.046 *
## income 1 340 21737 311 0.67 0.418
## years 1 2532 23928 315 4.97 0.031 *
## public 1 20 21417 310 0.04 0.844
## expend 1 10964 32361 330 21.52 3.4e-05 ***
## rank 1 2679 24076 316 5.26 0.027 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## Single term deletions
##
## Model:
## sat ~ ltakers + income + years + expend + rank
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 21417 310
## ltakers 1 2552 23968 313 5.12 0.029 *
## income 1 505 21922 309 1.01 0.319
## years 1 3011 24428 314 6.05 0.018 *
## expend 1 12465 33882 330 25.03 1e-05 ***
## rank 1 3162 24578 315 6.35 0.016 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1If you add1 here (to see if it makes sense to add either public or income back), neither is significant.
## Single term deletions
##
## Model:
## sat ~ ltakers + years + expend + rank
## Df Sum of Sq RSS AIC F value Pr(>F)
## <none> 21922 309
## ltakers 1 5094 27016 317 10.22 0.0026 **
## years 1 2870 24792 313 5.76 0.0207 *
## expend 1 13620 35542 331 27.34 4.5e-06 ***
## rank 1 2676 24598 313 5.37 0.0252 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Forward Stepwise: AIC
# lives in the base R stats package, but can be overwritten by other functions
stats::step(lm(sat ~ 1, data=sat_data),
sat ~ ltakers + income + years + public + expend + rank,
direction = "forward")## Start: AIC=419
## sat ~ 1
##
## Df Sum of Sq RSS AIC
## + ltakers 1 199007 46369 340
## + rank 1 190297 55079 348
## + income 1 102026 143350 395
## + years 1 26338 219038 416
## <none> 245376 419
## + public 1 1232 244144 421
## + expend 1 386 244991 421
##
## Step: AIC=340
## sat ~ ltakers
##
## Df Sum of Sq RSS AIC
## + expend 1 20523 25846 313
## + years 1 6364 40006 335
## <none> 46369 340
## + rank 1 871 45498 341
## + income 1 785 45584 341
## + public 1 449 45920 341
##
## Step: AIC=313
## sat ~ ltakers + expend
##
## Df Sum of Sq RSS AIC
## + years 1 1248 24598 313
## + rank 1 1054 24792 313
## <none> 25846 313
## + income 1 53 25792 315
## + public 1 1 25845 315
##
## Step: AIC=313
## sat ~ ltakers + expend + years
##
## Df Sum of Sq RSS AIC
## + rank 1 2676 21922 309
## <none> 24598 313
## + public 1 288 24310 314
## + income 1 19 24578 315
##
## Step: AIC=309
## sat ~ ltakers + expend + years + rank
##
## Df Sum of Sq RSS AIC
## <none> 21922 309
## + income 1 505 21417 310
## + public 1 185 21737 311##
## Call:
## lm(formula = sat ~ ltakers + expend + years + rank, data = sat_data)
##
## Coefficients:
## (Intercept) ltakers expend years rank
## 399.1 -38.1 4.0 13.1 4.4Backward Stepwise: BIC
# lives in the base R stats package, but can be overwritten by other functions
stats::step(lm(sat ~ (ltakers + income + years + public + expend + rank),
data=sat_data),
direction = "backward", k=log(sat_n))## Start: AIC=325
## sat ~ (ltakers + income + years + public + expend + rank)
##
## Df Sum of Sq RSS AIC
## - public 1 20 21417 321
## - income 1 340 21737 322
## <none> 21397 325
## - ltakers 1 2150 23547 326
## - years 1 2532 23928 327
## - rank 1 2679 24076 327
## - expend 1 10964 32361 342
##
## Step: AIC=321
## sat ~ ltakers + income + years + expend + rank
##
## Df Sum of Sq RSS AIC
## - income 1 505 21922 319
## <none> 21417 321
## - ltakers 1 2552 23968 323
## - years 1 3011 24428 324
## - rank 1 3162 24578 324
## - expend 1 12465 33882 340
##
## Step: AIC=319
## sat ~ ltakers + years + expend + rank
##
## Df Sum of Sq RSS AIC
## <none> 21922 319
## - rank 1 2676 24598 320
## - years 1 2870 24792 321
## - ltakers 1 5094 27016 325
## - expend 1 13620 35542 338##
## Call:
## lm(formula = sat ~ ltakers + years + expend + rank, data = sat_data)
##
## Coefficients:
## (Intercept) ltakers years expend rank
## 399.1 -38.1 13.1 4.0 4.4To get an idea of how complicated your models can get, try this:
step(lm(sat ~ (ltakers + income + years + public + expend + rank)^2),
direction = "backward")