10 Modeling as a Process

10.1 Comparing Models⁶

So many models, so little time. Understanding how to interpret a multiple linear regression model is only half of the modeling process. In most real-life situations, there are many variables which can be used to predict or describe the response variable at hand. But how to choose which combination or subset of variables is best?

Here, we’ll walk through many of the big ideas surrounding the modeling building process. In the next chapter we will consider the technical ideas behind statistical inference for modeling building. But even when using formal inference, the ideas here should always inform the larger process and analysis conclusions.

Leo Breiman was among the giants in machine learning who helped to bridge ideas in statistics and computer science. Trained as a statistician, he spent his career at the University of California, Berkeley where he developed Classification and Regression Trees (CART), bagging, and Random Forests.

Among his important insights was an idea that there are two cultures which can motivate (linear) modeling:

Think of the data as being generated by a black box in which a vector of input variables x (independent variables) go in one side, and on the other side the response variables y come out. Inside the black box, nature functions to associate the predictor variables with the response variables.

1. Data Modeling: The analysis in this culture starts with assuming a stochastic data model for the inside of the black box…The values of the parameters are estimated from the data and the model then used for information and/or prediction

2. Algorithmic Modeling: The analysis in this culture considers the inside of the box complex and unknown. [The] approach is to find a function f(x) — an algorithm that operates on x to predict the responses y.

Here in Chapter 10, the focus will be on algorithmic modeling and developing models which are optimally predictive of the response variable at hand.

Spoiler:

• In Chapter 11, the model building will use hypothesis testing and p-values.
• In Chapter 14, the model building will use mathematical optimization.

There isn’t a right way to model. In fact, good data analysis is hard. You are building a tool box. Make sure to notice that not every tool is the same, and you have more than just one hammer to use. Sometimes the tools can work together to form even better models.

Worth a comment

Notice that the R code has gotten more interesting now. How fun!! The R code will help the process! The R package tidymodels includes tools to facilitate, in particular, feature engineering and cross validation.

Bias-variance trade-off

Excellent resource

for explaining the bias-variance trade-off: http://scott.fortmann-roe.com/docs/BiasVariance.html

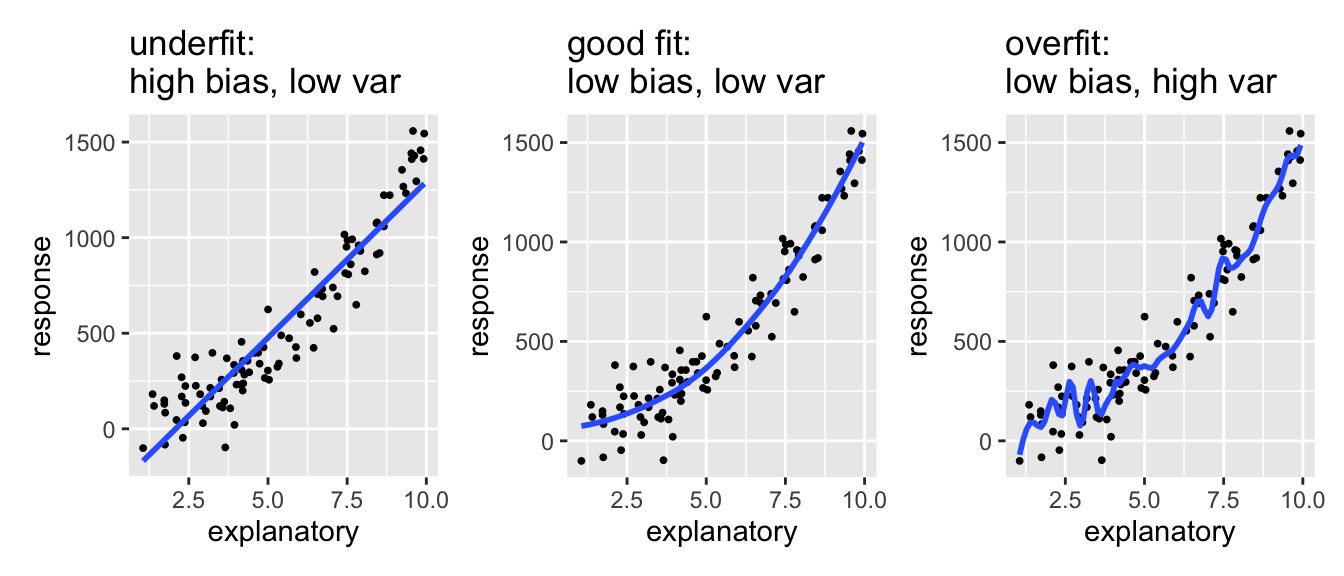
• Variance refers to the amount by which \(\hat{f}\) would change if we estimated it using a different training set. Generally, the closer the model fits the data, the more variable it will be (it’ll be different for each data set!). A model with many many explanatory variables will often fit the data too closely.

• Bias refers to the error that is introduced by approximating the “truth” by a model which is too simple. For example, we often use linear models to describe complex relationships, but it is unlikely that any real life situation actually has a true linear model. However, if the true relationship is close to linear, then the linear model will have a low bias.

Generally, the simpler the model, the lower the variance. The more complicated the model, the lower the bias. In this class, cross validation will be used to assess model fit with metrics of \(R^2\) and RMSE.

\[\begin{align} \mbox{prediction error } = \mbox{ irreducible error } + \mbox{ bias } + \mbox{ variance} \end{align}\]

• irreducible error The irreducible error is the natural variability that comes with observations. No matter how good the model is, we will never be able to predict perfectly.
• bias The bias of the model represents the difference between the true model and a model which is too simple. That is, the more complicated the model (e.g., the more variables), the closer the points are to the prediction. As the model gets more complicated (e.g., as variables are added), the bias goes down.
• variance The variance represents the variability of the model from sample to sample. That is, a simple model (very few variables) would not change a lot from sample to sample. The variance decreases as the model becomes more simple (e.g., variables are removed).

Note the bias-variance trade-off. We want our prediction error to be small, so we choose a model that is medium with respect to both bias and variance. We cannot control the irreducible error.

Figure 1.3: Test and training error as a function of model complexity. Note that the error goes down monotonically only for the training data. Be careful not to overfit!! (T. Hastie, Tibshirani, and Friedman 2001)

10.2 Feature Engineering

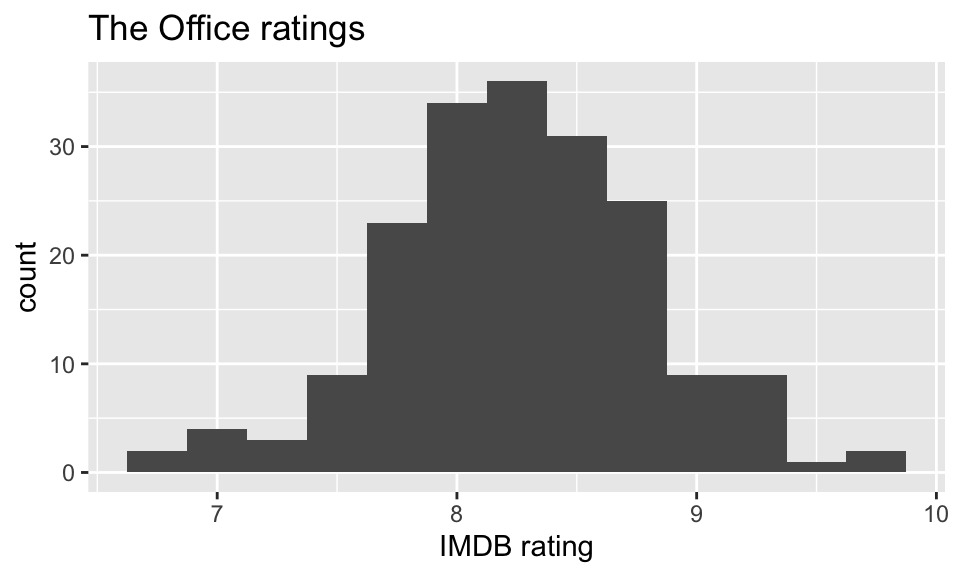
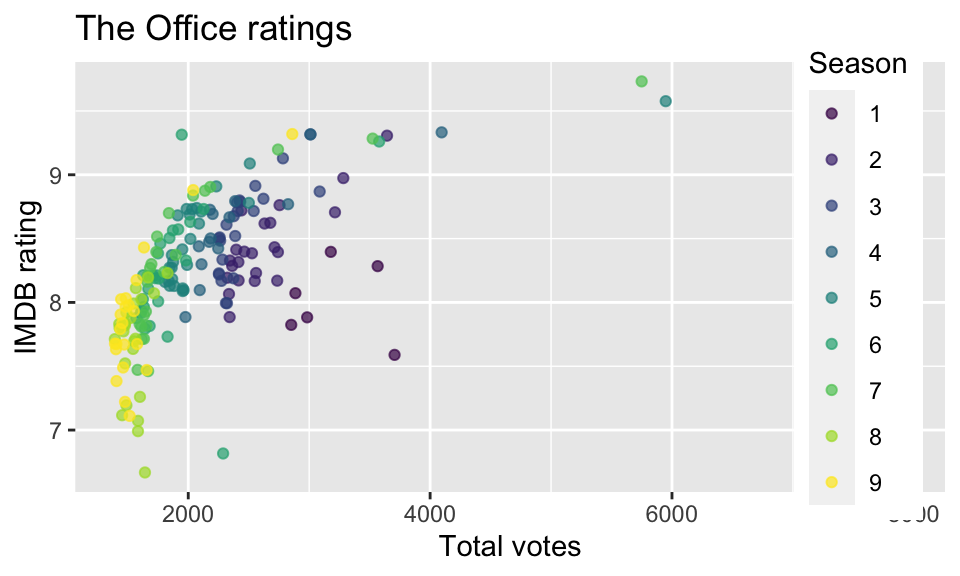
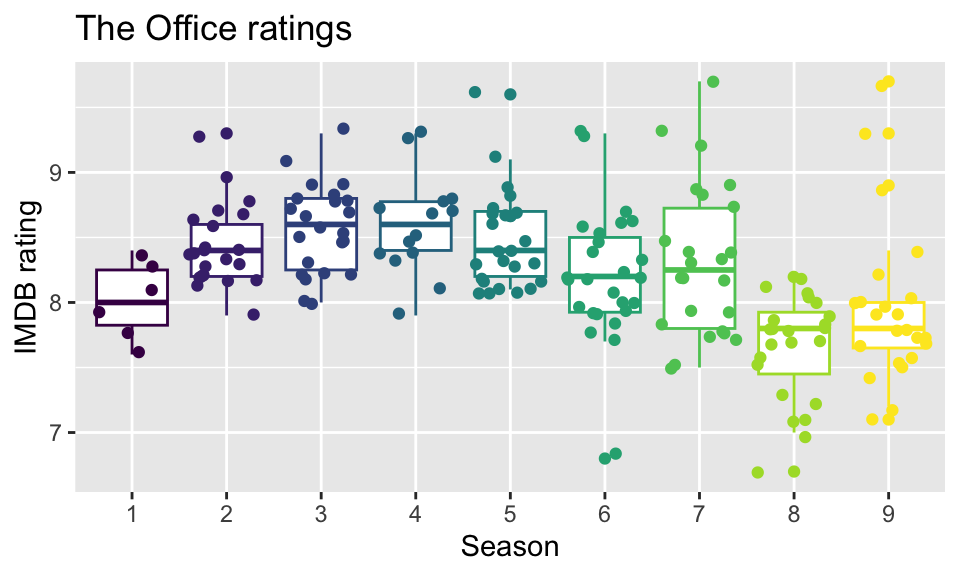
For the example used to consider feature engineering, the data come from data.world, by way of TidyTuesday. They now exist in the schrute R package.

Can the IMDB rating (imdb_rating) for The Office be predicted from the other variables in the dataset? Which model is best?

Instead of jumping into the predictions immediately, let’s look at the data itself. What wrangling can we do to the data in order to take advantage of all the information in the variables? We’d also like to make the model accurate and easy to communicate.

## # A tibble: 188 × 6
##    season episode title             imdb_rating total_votes air_date  
##     <dbl>   <dbl> <chr>                   <dbl>       <dbl> <date>    
##  1      1       1 Pilot                     7.6        3706 2005-03-24
##  2      1       2 Diversity Day             8.3        3566 2005-03-29
##  3      1       3 Health Care               7.9        2983 2005-04-05
##  4      1       4 The Alliance              8.1        2886 2005-04-12
##  5      1       5 Basketball                8.4        3179 2005-04-19
##  6      1       6 Hot Girl                  7.8        2852 2005-04-26
##  7      2       1 The Dundies               8.7        3213 2005-09-20
##  8      2       2 Sexual Harassment         8.2        2736 2005-09-27
##  9      2       3 Office Olympics           8.4        2742 2005-10-04
## 10      2       4 The Fire                  8.4        2713 2005-10-11
## # … with 178 more rows

IMDB ratings

IMDB ratings vs. number of votes

Outliers?

Aside…

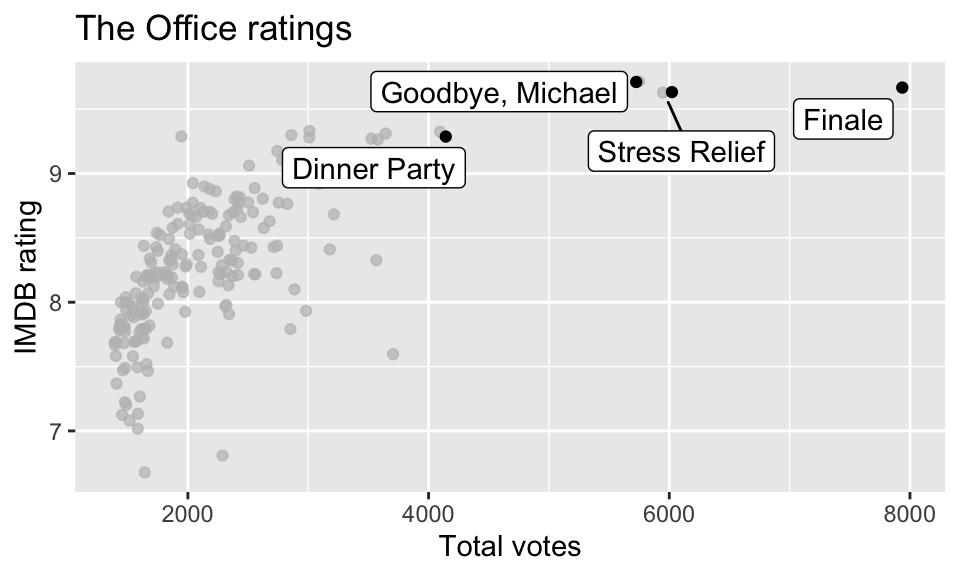
If you like the Dinner Party episode, I highly recommend this “oral history” of the episode published on Rolling Stone magazine.

Rating vs. air date

IMDB ratings vs. seasons

10.2.1 Building a Model

If the idea is to build a model which can predict IMDB ratings, we need to have a way to see how we did (at the end). Indeed, it is important for us to put some data in our pocket (it will be called the “test” data) which doesn’t see any of the modeling process. We’ll use the test data at the end to assess whether or not our predictions are any good.

Train / test

Step 1: Create an initial split:

set.seed(123)
office_split <- initial_split(office_ratings) # prop = 3/4 by default

Step 2: Save training data

office_train <- training(office_split)
dim(office_train)

## [1] 141   6

Step 3: Save testing data

office_test  <- testing(office_split)
dim(office_test)

## [1] 47  6

Using the training data

office_train

## # A tibble: 141 × 6
##    season episode title               imdb_rating total_votes air_date  
##     <dbl>   <dbl> <chr>                     <dbl>       <dbl> <date>    
##  1      8      18 Last Day in Florida         7.8        1429 2012-03-08
##  2      9      14 Vandalism                   7.6        1402 2013-01-31
##  3      2       8 Performance Review          8.2        2416 2005-11-15
##  4      9       5 Here Comes Treble           7.1        1515 2012-10-25
##  5      3      22 Beach Games                 9.1        2783 2007-05-10
##  6      7       1 Nepotism                    8.4        1897 2010-09-23
##  7      3      15 Phyllis' Wedding            8.3        2283 2007-02-08
##  8      9      21 Livin' the Dream            8.9        2041 2013-05-02
##  9      9      18 Promos                      8          1445 2013-04-04
## 10      8      12 Pool Party                  8          1612 2012-01-19
## # … with 131 more rows

10.2.2 Feature engineering

• We prefer simple models when possible, but parsimony does not mean sacrificing accuracy (or predictive performance) in the interest of simplicity.

• Variables that go into the model and how they are represented are just as critical to success of the model.

• Feature engineering allows us to get creative with our predictors in an effort to make them more useful for our model (to increase its predictive performance).

Feature engineering is the process of transforming raw data into features (variables) that are better predictors (for the model at hand).

Feature engineering with dplyr

We can use the dplyr (in tidyverse) and, for example, the mutate() function to create new variables to use in the models.

office_train %>%
  mutate(
    season = as_factor(season),
    month = lubridate::month(air_date),
    wday = lubridate::wday(air_date)
  )

## # A tibble: 141 × 8
##   season episode title               imdb_rating total_…¹ air_date   month  wday
##   <fct>    <dbl> <chr>                     <dbl>    <dbl> <date>     <dbl> <dbl>
## 1 8           18 Last Day in Florida         7.8     1429 2012-03-08     3     5
## 2 9           14 Vandalism                   7.6     1402 2013-01-31     1     5
## 3 2            8 Performance Review          8.2     2416 2005-11-15    11     3
## 4 9            5 Here Comes Treble           7.1     1515 2012-10-25    10     5
## 5 3           22 Beach Games                 9.1     2783 2007-05-10     5     5
## 6 7            1 Nepotism                    8.4     1897 2010-09-23     9     5
## # … with 135 more rows, and abbreviated variable name ¹​total_votes

Can you identify any potential problems with this approach?

One of the problems is that with the mutate() approach the test and training data get formatted separately so there might be inconsistencies when the test data are predicted at the end.

Modeling workflow

Ideally, the feature engineering happens as part of the workflow. That is, part of the modeling process. That way, when the training data is used to fit the model, feature engineering happens. When the test data is used to come up with predictions, feature engineering also happens.

• Create a recipe for feature engineering steps to be applied to the training data

• Fit the model to the training data after these steps have been applied

• Use the model estimates from the training data, predict outcomes for the test data

• Evaluate the performance of the model on the test data

The process is synthesized in the following graphic from a course at Johns Hopkins, Tidyverse Skills for Data Science.

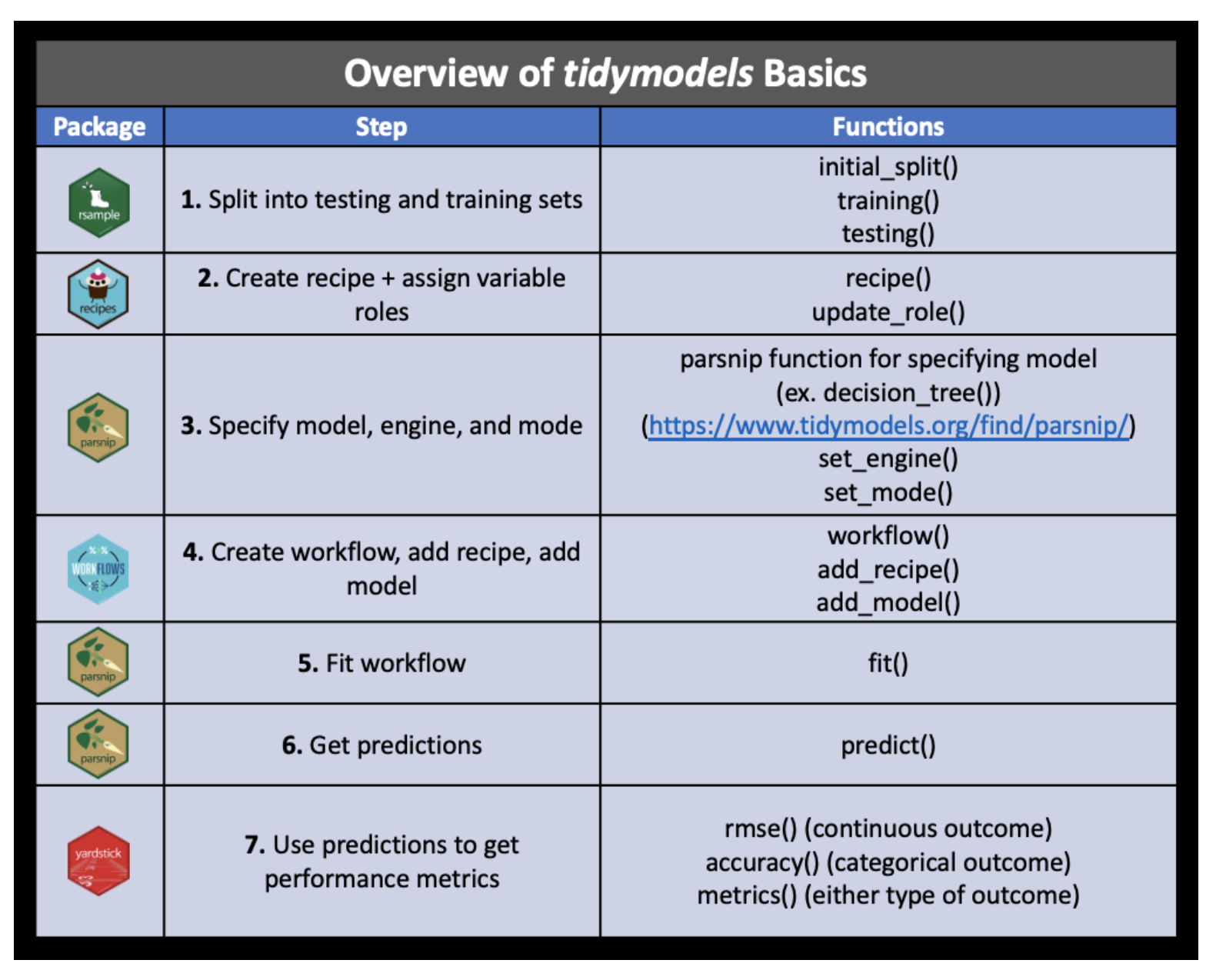
Figure 10.1: Image credit: Wright et al., Chapter 5 of Tidyverse Skills for Data Science https://jhudatascience.org/tidyversecourse/

10.2.3 Specifying a model

Instead of using the lm() command, we’re going to use the tidymodels framework to specify a model. In Math 158 we will always use “lm” as the engine, but if you take other applied statistics classes, you’ll use different model specifications with the same feature engineering and modeling fitting steps.

office_spec <- linear_reg() %>%
  set_engine("lm")

office_spec

## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

10.2.4 Building a recipe

The steps in building a recipe are done sequentially so that the format of each variable is as desired for the model. As seen in Section (@ref{sec:wflow}), the recipe steps can happen in sequence using the pipe (%>%) function.

However, when you work with a single pipeline, the recipe effects on the data aren’t seen, which can be unsettling. You can look at what will happen when you ultimately apply the recipe to your data by using the functions prep() and bake().

Note: Using prep() and bake() are shown here for demonstrative purposes. They do not need to be a part of your pipeline. I do find them assuring, however, so that I can see the effects of the recipe steps as the recipe is built.

Initiate a recipe

office_rec <- recipe(
  imdb_rating ~ .,    # formula
  data = office_train # data for cataloging names and types of variables
  )

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##    outcome          1
##  predictor          5

Step 1: Alter roles

title isn’t a predictor, but we might want to keep it around as an ID.

update_role() alters an existing role in the recipe or assigns an initial role to variables that do not yet have a declared role.

office_rec <- office_rec %>%
  update_role(title, new_role = "ID")

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 6
## $ season      <dbl> 8, 9, 2, 9, 3, 7, 3, 9, 9, 8, 5, 5, 9, 6, 7, 6, 5, 2, 2, 9…
## $ episode     <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26, 12, 1, 20, 8,…
## $ title       <fct> "Last Day in Florida", "Vandalism", "Performance Review", …
## $ total_votes <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2041, 1445, 1612…
## $ air_date    <date> 2012-03-08, 2013-01-31, 2005-11-15, 2012-10-25, 2007-05-1…
## $ imdb_rating <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0, 8.0, 8.7, 8.9…

Step 2: Add features

New features for day of week and month. Here, the air_date variable is being specified to keep separate information on both the day of week and the month information.

step_date() creates a specification of a recipe step that will convert date data into one or more factor or numeric variables.

office_rec <- office_rec %>%
  step_date(air_date, features = c("dow", "month"))

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 8
## $ season         <dbl> 8, 9, 2, 9, 3, 7, 3, 9, 9, 8, 5, 5, 9, 6, 7, 6, 5, 2, 2…
## $ episode        <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26, 12, 1, 20,…
## $ title          <fct> "Last Day in Florida", "Vandalism", "Performance Review…
## $ total_votes    <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2041, 1445, 1…
## $ air_date       <date> 2012-03-08, 2013-01-31, 2005-11-15, 2012-10-25, 2007-0…
## $ imdb_rating    <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0, 8.0, 8.7, …
## $ air_date_dow   <fct> Thu, Thu, Tue, Thu, Thu, Thu, Thu, Thu, Thu, Thu, Thu, …
## $ air_date_month <fct> Mar, Jan, Nov, Oct, May, Sep, Feb, May, Apr, Jan, May, …

Step 3: Add more features

Identify holidays in air_date, then remove air_date.

step_holiday() creates a specification of a recipe step that will convert date data into one or more binary indicator variables for common holidays.

office_rec <- office_rec %>%
  step_holiday(
    air_date, 
    holidays = c("USThanksgivingDay", "USChristmasDay", "USNewYearsDay", "USIndependenceDay"), 
    keep_original_cols = FALSE
  )

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date
## Holiday features from air_date

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 11
## $ season                     <dbl> 8, 9, 2, 9, 3, 7, 3, 9, 9, 8, 5, 5, 9, 6, 7…
## $ episode                    <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26…
## $ title                      <fct> "Last Day in Florida", "Vandalism", "Perfor…
## $ total_votes                <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2…
## $ imdb_rating                <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0…
## $ air_date_dow               <fct> Thu, Thu, Tue, Thu, Thu, Thu, Thu, Thu, Thu…
## $ air_date_month             <fct> Mar, Jan, Nov, Oct, May, Sep, Feb, May, Apr…
## $ air_date_USThanksgivingDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USChristmasDay    <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USNewYearsDay     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USIndependenceDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…

Step 4: Convert numbers to factors

Convert season to factor.

step_num2factor() will convert one or more numeric vectors to factors (ordered or unordered). This can be useful when categories are encoded as integers.

office_rec <- office_rec %>%
  step_num2factor(season, levels = as.character(1:9))

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date
## Holiday features from air_date
## Factor variables from season

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 11
## $ season                     <fct> 8, 9, 2, 9, 3, 7, 3, 9, 9, 8, 5, 5, 9, 6, 7…
## $ episode                    <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26…
## $ title                      <fct> "Last Day in Florida", "Vandalism", "Perfor…
## $ total_votes                <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2…
## $ imdb_rating                <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0…
## $ air_date_dow               <fct> Thu, Thu, Tue, Thu, Thu, Thu, Thu, Thu, Thu…
## $ air_date_month             <fct> Mar, Jan, Nov, Oct, May, Sep, Feb, May, Apr…
## $ air_date_USThanksgivingDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USChristmasDay    <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USNewYearsDay     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USIndependenceDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…

Step 5: Make dummy variables

Convert all nominal (categorical) predictors to factors.

step_dummy() creates a specification of a recipe step that will convert nominal data (e.g. character or factors) into one or more numeric binary model terms for the levels of the original data.

office_rec <- office_rec %>%
  step_dummy(all_nominal_predictors())

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date
## Holiday features from air_date
## Factor variables from season
## Dummy variables from all_nominal_predictors()

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 33
## $ episode                    <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26…
## $ title                      <fct> "Last Day in Florida", "Vandalism", "Perfor…
## $ total_votes                <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2…
## $ imdb_rating                <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0…
## $ air_date_USThanksgivingDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USChristmasDay    <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USNewYearsDay     <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_USIndependenceDay <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X2                  <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X3                  <dbl> 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X4                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X5                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0…
## $ season_X6                  <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0…
## $ season_X7                  <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1…
## $ season_X8                  <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0…
## $ season_X9                  <dbl> 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0…
## $ air_date_dow_Mon           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_dow_Tue           <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_dow_Wed           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_dow_Thu           <dbl> 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
## $ air_date_dow_Fri           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_dow_Sat           <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Feb         <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Mar         <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Apr         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1…
## $ air_date_month_May         <dbl> 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0…
## $ air_date_month_Jun         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Jul         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Aug         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Sep         <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0…
## $ air_date_month_Oct         <dbl> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Nov         <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ air_date_month_Dec         <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…

Step 6: Remove zero variance predictors

Remove all predictors that contain only a single value. “zero variance” means that there is no variability in the entire column, literally every value is the same. Those variables won’t ever help with prediction.

step_zv() creates a specification of a recipe step that will remove variables that contain only a single value.

office_rec <- office_rec %>%
  step_zv(all_predictors())

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date
## Holiday features from air_date
## Factor variables from season
## Dummy variables from all_nominal_predictors()
## Zero variance filter on all_predictors()

office_rec_trained <- prep(office_rec)

bake(office_rec_trained, office_train) %>%
  glimpse

## Rows: 141
## Columns: 22
## $ episode            <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26, 12, 1,…
## $ title              <fct> "Last Day in Florida", "Vandalism", "Performance Re…
## $ total_votes        <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2041, 144…
## $ imdb_rating        <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0, 8.0, 8…
## $ season_X2          <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ season_X3          <dbl> 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ season_X4          <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ season_X5          <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, …
## $ season_X6          <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, …
## $ season_X7          <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, …
## $ season_X8          <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, …
## $ season_X9          <dbl> 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, …
## $ air_date_dow_Tue   <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ air_date_dow_Thu   <dbl> 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
## $ air_date_month_Feb <dbl> 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ air_date_month_Mar <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
## $ air_date_month_Apr <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, …
## $ air_date_month_May <dbl> 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, …
## $ air_date_month_Sep <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, …
## $ air_date_month_Oct <dbl> 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, …
## $ air_date_month_Nov <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, …
## $ air_date_month_Dec <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, …

Putting it altogether

Turns out that all of the feature engineering steps can do using the pipe function (%>%) to concatenate the functions.

office_rec <- recipe(imdb_rating ~ ., data = office_train) %>%
  # make title's role ID
  update_role(title, new_role = "ID") %>%
  # extract day of week and month of air_date
  step_date(air_date, features = c("dow", "month")) %>%
  # identify holidays and add indicators
  step_holiday(
    air_date, 
    holidays = c("USThanksgivingDay", "USChristmasDay", "USNewYearsDay", "USIndependenceDay"), 
    keep_original_cols = FALSE
  ) %>%
  # turn season into factor
  step_num2factor(season, levels = as.character(1:9)) %>%
  # make dummy variables
  step_dummy(all_nominal_predictors()) %>%
  # remove zero variance predictors
  step_zv(all_predictors())

office_rec

## Recipe
## 
## Inputs:
## 
##       role #variables
##         ID          1
##    outcome          1
##  predictor          4
## 
## Operations:
## 
## Date features from air_date
## Holiday features from air_date
## Factor variables from season
## Dummy variables from all_nominal_predictors()
## Zero variance filter on all_predictors()

step_ functions

For more information: https://recipes.tidymodels.org/reference/index.html

ls(pattern = '^step_', env = as.environment('package:recipes'))

##  [1] "step_arrange"            "step_bagimpute"         
##  [3] "step_bin2factor"         "step_BoxCox"            
##  [5] "step_bs"                 "step_center"            
##  [7] "step_classdist"          "step_corr"              
##  [9] "step_count"              "step_cut"               
## [11] "step_date"               "step_depth"             
## [13] "step_discretize"         "step_dummy"             
## [15] "step_dummy_extract"      "step_dummy_multi_choice"
## [17] "step_factor2string"      "step_filter"            
## [19] "step_filter_missing"     "step_geodist"           
## [21] "step_harmonic"           "step_holiday"           
## [23] "step_hyperbolic"         "step_ica"               
## [25] "step_impute_bag"         "step_impute_knn"        
## [27] "step_impute_linear"      "step_impute_lower"      
## [29] "step_impute_mean"        "step_impute_median"     
## [31] "step_impute_mode"        "step_impute_roll"       
## [33] "step_indicate_na"        "step_integer"           
## [35] "step_interact"           "step_intercept"         
## [37] "step_inverse"            "step_invlogit"          
## [39] "step_isomap"             "step_knnimpute"         
## [41] "step_kpca"               "step_kpca_poly"         
## [43] "step_kpca_rbf"           "step_lag"               
## [45] "step_lincomb"            "step_log"               
## [47] "step_logit"              "step_lowerimpute"       
## [49] "step_meanimpute"         "step_medianimpute"      
## [51] "step_modeimpute"         "step_mutate"            
## [53] "step_mutate_at"          "step_naomit"            
## [55] "step_nnmf"               "step_nnmf_sparse"       
## [57] "step_normalize"          "step_novel"             
## [59] "step_ns"                 "step_num2factor"        
## [61] "step_nzv"                "step_ordinalscore"      
## [63] "step_other"              "step_pca"               
## [65] "step_percentile"         "step_pls"               
## [67] "step_poly"               "step_poly_bernstein"    
## [69] "step_profile"            "step_range"             
## [71] "step_ratio"              "step_regex"             
## [73] "step_relevel"            "step_relu"              
## [75] "step_rename"             "step_rename_at"         
## [77] "step_rm"                 "step_rollimpute"        
## [79] "step_sample"             "step_scale"             
## [81] "step_select"             "step_shuffle"           
## [83] "step_slice"              "step_spatialsign"       
## [85] "step_spline_b"           "step_spline_convex"     
## [87] "step_spline_monotone"    "step_spline_natural"    
## [89] "step_spline_nonnegative" "step_sqrt"              
## [91] "step_string2factor"      "step_time"              
## [93] "step_unknown"            "step_unorder"           
## [95] "step_window"             "step_YeoJohnson"        
## [97] "step_zv"

10.2.5 Building workflows

Workflows bring together models and recipes so that they can be easily applied to both the training and test data.

Specify model

office_spec <- linear_reg() %>%
  set_engine("lm")

office_spec

## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

The workflow: Notice that the two important parts to the workflows are the model specification and the feature engineering recipe information.

office_wflow <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec)

office_wflow

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: linear_reg()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 5 Recipe Steps
## 
## • step_date()
## • step_holiday()
## • step_num2factor()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

Fit model to training data

With the workflow in hand, the model can now be fit to the training data. Although, wow… there are so many predictors!

office_fit <- office_wflow %>%
  fit(data = office_train)

office_fit %>% tidy() %>% print(n = 21)

## # A tibble: 21 × 5
##    term                estimate std.error statistic  p.value
##    <chr>                  <dbl>     <dbl>     <dbl>    <dbl>
##  1 (Intercept)         6.40     0.510        12.5   1.51e-23
##  2 episode            -0.00393  0.0171       -0.230 8.18e- 1
##  3 total_votes         0.000375 0.0000414     9.07  2.75e-15
##  4 season_X2           0.811    0.327         2.48  1.44e- 2
##  5 season_X3           1.04     0.343         3.04  2.91e- 3
##  6 season_X4           1.09     0.295         3.70  3.32e- 4
##  7 season_X5           1.08     0.348         3.11  2.34e- 3
##  8 season_X6           1.00     0.367         2.74  7.18e- 3
##  9 season_X7           1.02     0.352         2.89  4.52e- 3
## 10 season_X8           0.497    0.348         1.43  1.55e- 1
## 11 season_X9           0.621    0.345         1.80  7.41e- 2
## 12 air_date_dow_Tue    0.382    0.422         0.904 3.68e- 1
## 13 air_date_dow_Thu    0.284    0.389         0.731 4.66e- 1
## 14 air_date_month_Feb -0.0597   0.132        -0.452 6.52e- 1
## 15 air_date_month_Mar -0.0752   0.156        -0.481 6.31e- 1
## 16 air_date_month_Apr  0.0954   0.177         0.539 5.91e- 1
## 17 air_date_month_May  0.156    0.213         0.734 4.64e- 1
## 18 air_date_month_Sep -0.0776   0.223        -0.348 7.28e- 1
## 19 air_date_month_Oct -0.176    0.174        -1.01  3.13e- 1
## 20 air_date_month_Nov -0.156    0.149        -1.05  2.98e- 1
## 21 air_date_month_Dec  0.170    0.149         1.14  2.55e- 1

10.2.6 Evaluate the model

Predictions for training data

office_train_pred <- predict(office_fit, office_train) %>%
  bind_cols(office_train %>% select(imdb_rating, title))

office_train_pred

## # A tibble: 141 × 3
##    .pred imdb_rating title              
##    <dbl>       <dbl> <chr>              
##  1  7.57         7.8 Last Day in Florida
##  2  7.77         7.6 Vandalism          
##  3  8.31         8.2 Performance Review 
##  4  7.67         7.1 Here Comes Treble  
##  5  8.84         9.1 Beach Games        
##  6  8.33         8.4 Nepotism           
##  7  8.46         8.3 Phyllis' Wedding   
##  8  8.14         8.9 Livin' the Dream   
##  9  7.87         8   Promos             
## 10  7.74         8   Pool Party         
## # … with 131 more rows

R-squared

Percentage of variability in the IMDB ratings explained by the model.

rsq(office_train_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rsq     standard       0.670

Are models with high or low \(R^2\) more preferable?

RMSE

An alternative model performance statistic: root mean square error.

\[RMSE = \sqrt{\frac{\sum_{i = 1}^n (y_i - \hat{y}_i)^2}{n}}\] Note: RMSE here is computed as it would be for any type of statistics or machine learning model (i.e., how far are the typical observations from the predicted value). The change in denominator means that the MSE with \(n\) won’t estimate \(\sigma^2\), but it also means that the metric allows us to compare different kinds of models (e.g., a linear regression vs. neural network vs. random forest) on the same scale. And yes, this MSE will decrease as the number of parameters increases which is why we use cross validation or F-tests to constrain the model.

• Are models with high or low RMSE are more preferable?
• Is this RMSE considered low or high?

rmse(office_train_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       0.302

Depends…

office_train %>%
  summarise(min = min(imdb_rating), 
            max = max(imdb_rating))

## # A tibble: 1 × 2
##     min   max
##   <dbl> <dbl>
## 1   6.7   9.7

But, really…

who cares about predictions on training data?

Predictions for testing data

office_test_pred <- predict(office_fit, office_test) %>%
  bind_cols(office_test %>% select(imdb_rating, title))

office_test_pred

## # A tibble: 47 × 3
##    .pred imdb_rating title              
##    <dbl>       <dbl> <chr>              
##  1  8.03         8.3 Diversity Day      
##  2  7.98         7.9 Health Care        
##  3  8.41         8.4 The Fire           
##  4  8.35         8.2 Halloween          
##  5  8.35         8.4 E-Mail Surveillance
##  6  8.68         9   The Injury         
##  7  8.32         7.9 The Carpet         
##  8  8.93         9.3 Casino Night       
##  9  8.80         8.9 Gay Witch Hunt     
## 10  8.37         8.2 Initiation         
## # … with 37 more rows

Evaluate performance for testing data

\(R^2\) of model fit to testing data

rsq(office_test_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rsq     standard       0.468

RMSE of model fit to testing data

rmse(office_test_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       0.411

Training vs. testing

rmse_train <- rmse(office_train_pred, truth = imdb_rating, estimate = .pred) %>%
  pull(.estimate) %>%
  round(3)

rsq_train <- rsq(office_train_pred, truth = imdb_rating, estimate = .pred) %>%
  pull(.estimate) %>%
  round(3)

rmse_test <- rmse(office_test_pred, truth = imdb_rating, estimate = .pred) %>%
  pull(.estimate) %>%
  round(3)

rsq_test <- rsq(office_test_pred, truth = imdb_rating, estimate = .pred) %>%
  pull(.estimate) %>%
  round(3)

metric	train	test	comparison
RMSE	0.302	0.411	RMSE lower for training
R-squared	0.67	0.468	R-squared higher for training

Evaluating performance on training data

• The training set does not have the capacity to be a good arbiter of performance.

• It is not an independent piece of information; predicting the training set can only reflect what the model already knows.

• Suppose you give a class a test, then give them the answers, then provide the same test. The student scores on the second test do not accurately reflect what they know about the subject; these scores would probably be higher than their results on the first test.

10.3 Cross Validation

Before we get into the details of cross validation, let’s set up the scenario for when we need cross validation. Recall that we use the test data to assess how the model does. But we haven’t yet thought about how to use the data to build a particular model.

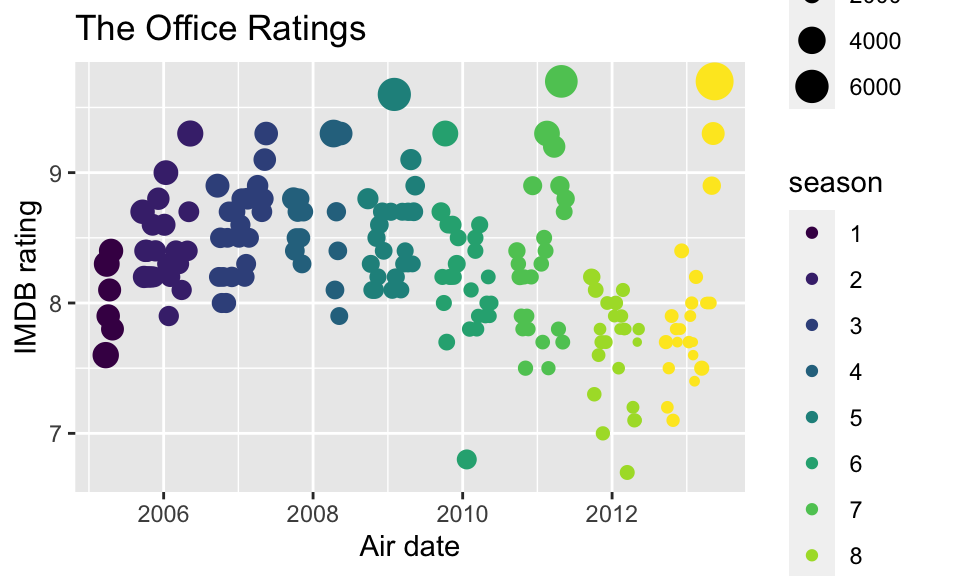
For example, let’s set up a scenario to compare two different models. The first model doesn’t use air_date at all but is otherwise similar to the model above. The second model does also not use air_date as a variable and considers season as a numeric variable.

Model 1:

office_rec1 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "ID") %>%
  # delete the air_date variable
  step_rm(air_date) %>%
  step_num2factor(season, levels = as.character(1:9)) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

prep(office_rec1) %>%
bake(office_train) %>%
  glimpse()

## Rows: 141
## Columns: 12
## $ episode     <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26, 12, 1, 20, 8,…
## $ title       <fct> "Last Day in Florida", "Vandalism", "Performance Review", …
## $ total_votes <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2041, 1445, 1612…
## $ imdb_rating <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0, 8.0, 8.7, 8.9…
## $ season_X2   <dbl> 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0…
## $ season_X3   <dbl> 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X4   <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X5   <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0…
## $ season_X6   <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0…
## $ season_X7   <dbl> 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0…
## $ season_X8   <dbl> 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
## $ season_X9   <dbl> 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1…

Model 2:

office_rec2 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "id") %>%
  # delete the air_date variable
  step_rm(air_date) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

prep(office_rec2) %>%
bake(office_train) %>%
  glimpse()

## Rows: 141
## Columns: 5
## $ season      <dbl> 8, 9, 2, 9, 3, 7, 3, 9, 9, 8, 5, 5, 9, 6, 7, 6, 5, 2, 2, 9…
## $ episode     <dbl> 18, 14, 8, 5, 22, 1, 15, 21, 18, 12, 25, 26, 12, 1, 20, 8,…
## $ title       <fct> "Last Day in Florida", "Vandalism", "Performance Review", …
## $ total_votes <dbl> 1429, 1402, 2416, 1515, 2783, 1897, 2283, 2041, 1445, 1612…
## $ imdb_rating <dbl> 7.8, 7.6, 8.2, 7.1, 9.1, 8.4, 8.3, 8.9, 8.0, 8.0, 8.7, 8.9…

Creating workflows

Using each of the separate recipes, different workflows are set up:

Model 1:

office_wflow1 <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec1)

office_wflow1

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: linear_reg()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 4 Recipe Steps
## 
## • step_rm()
## • step_num2factor()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

Model 2:

office_wflow2 <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec2)

office_wflow2

## ══ Workflow ════════════════════════════════════════════════════════════════════
## Preprocessor: Recipe
## Model: linear_reg()
## 
## ── Preprocessor ────────────────────────────────────────────────────────────────
## 3 Recipe Steps
## 
## • step_rm()
## • step_dummy()
## • step_zv()
## 
## ── Model ───────────────────────────────────────────────────────────────────────
## Linear Regression Model Specification (regression)
## 
## Computational engine: lm

Fit the models to the training data

WAIT, not so fast!

Implementing Cross Validation

Figure 10.2: (Flach 2012)

Cross validation is typically used in two ways.

1. To assess a model’s accuracy (model assessment).
   
2. To build a model (model selection).

10.3.1 Different ways to CV

Suppose that we build a classifier on a given data set. We’d like to know how well the model classifies observations, but if we test on the samples at hand, the error rate will be much lower than the model’s inherent accuracy rate. Instead, we’d like to predict new observations that were not used to create the model. There are various ways of creating test or validation sets of data:

• one training set, one test set [two drawbacks: estimate of error is highly variable because it depends on which points go into the training set; and because the training data set is smaller than the full data set, the error rate is biased in such a way that it overestimates the actual error rate of the modeling technique.]

• leave one out cross validation (LOOCV)

1. remove one observation
2. build the model using the remaining n-1 points
3. predict class membership for the observation which was removed
4. repeat by removing each observation one at a time

• \(V\)-fold cross validation (\(V\)-fold CV)
  • like LOOCV except that the algorithm is run \(V\) times on each group (of approximately equal size) from a partition of the data set.]
  • LOOCV is a special case of \(V\)-fold CV with \(V=n\)
  • advantage of \(V\)-fold is computational
  • \(V\)-fold often has a better bias-variance trade-off [bias is lower with LOOCV. however, because LOOCV predicts \(n\) observations from \(n\) models which are basically the same, the variability will be higher (i.e., based on the \(n\) data values). with \(V\)-fold, prediction is on \(n\) values from \(V\) models which are much less correlated. the effect is to average out the predicted values in such a way that there will be less variability from data set to data set.]

CV for Model assessment 10-fold

1. assume variables are set
2. remove 10% of the data
3. build the model using the remaining 90%
4. predict response for the 10% of the observations which were removed
5. repeat by removing each decile one at a time
6. a good measure of the model’s ability to predict is the error rate associated with the predictions on the data which have been independently predicted

CV for Model selection 10-fold

1. set the variables
2. build the model using the variables set above:
   1. remove 10% of the data
   2. build the model using the remaining 90%
   3. predict response for the 10% of the observations which were removed
   4. repeat by removing each decile one at a time
3. measure the CV prediction error for the \(k\) value at hand
4. repeat steps 1-3 and choose the variables for which the prediction error is lowest

CV for Model assessment and selection 10-fold

To do both, one approach is to use test/training data and CV in order to both model assessment and selection. Note that CV could be used in both steps, but the algorithm is slightly more complicated.

1. split the data into training and test observations
2. set \(k\) in \(k\)-NN
3. build the model using the \(k\) value set above on only the training data:
   1. remove 10% of the training data
   2. build the model using the remaining 90% of the training data
   3. predict class membership / continuous response for the 10% of the training observations which were removed
   4. repeat by removing each decile one at a time from the training data
4. measure the CV prediction error for the \(k\) value at hand on the training data
5. repeat steps 2-4 and choose the \(k\) for which the prediction error is lowest for the training data
6. using the \(k\) value given in step 5, assess the prediction error on the test data

Figure 10.3: Nested cross-validation: two cross-validation loops are run one inside the other. (Varoquaux et al. 2017)

10.3.2 Fit the models using cross validation

“Spending” the data

• We have already established that the idea of data spending where the test set was recommended for obtaining an unbiased estimate of performance.
• However, we need to decide which model to choose before using the test set.
• Typically we can’t decide on which final model to take to the test set without making model assessments.
• Remedy: Resampling to make model assessments on training data in a way that can generalize to new data.

Resampling for model assessment

Resampling is only conducted on the training set. The test set is not involved. For each iteration of resampling, the data are partitioned into two subsamples:

• The model is fit with the analysis set.
• The model is evaluated with the assessment set.

Figure 10.4: Repeated samples are taken from the training data, and with each resample some of the observations are used to build a model and some observations are used to estimate the performance. Source: (Kuhn and Silge 2022)

Aside: the “re” in “resamples” is for repeated samples. Not to be confused where repeated samples are taken in bootstrapping with replacement. In cross validation, the repeated samples are taken without replacement.

Analysis and assessment sets

• Analysis set is analogous to training set.
• Assessment set is analogous to test set.
• The terms analysis and assessment avoids confusion with initial split of the data.
• These data sets are mutually exclusive.

Cross validation

More specifically, v-fold cross validation – commonly used resampling technique:

• Randomly split your training data into v partitions
• Use 1 partition for assessment, and the remaining v-1 partitions for analysis
• Repeat v times, updating which partition is used for assessment each time

Let’s give an example where v = 3…

Cross validation, step 1

Consider the example below where the training data are randomly split into 3 partitions:

Figure 10.5: Splitting the data into a partition of v=3 groups. Source: (Kuhn and Silge 2022)

set.seed(345)
folds <- vfold_cv(office_train, v = 3)
folds

## #  3-fold cross-validation 
## # A tibble: 3 × 2
##   splits          id   
##   <list>          <chr>
## 1 <split [94/47]> Fold1
## 2 <split [94/47]> Fold2
## 3 <split [94/47]> Fold3

Note that the three repeated samples (“resamples”) are taken without replacement from the original dataset.

Cross validation, steps 2 and 3

• Use 1 partition for assessment, and the remaining v-1 partitions for analysis
• Repeat v times, updating which partition is used for assessment each time

Figure 10.6: With the data split into three groups, we can see how 2/3 of the observations are used to fit the model and 1/3 of the observations are used to estimate the performance of the model. Source: (Kuhn and Silge 2022)

Fit resamples

After the data have been split into v (here 3) resamples, they can each be fit to the two models of interest.

Model 1:

set.seed(456)

office_fit_rs1 <- office_wflow1 %>%
  fit_resamples(folds)

office_fit_rs1

## # Resampling results
## # 3-fold cross-validation 
## # A tibble: 3 × 4
##   splits          id    .metrics         .notes          
##   <list>          <chr> <list>           <list>          
## 1 <split [94/47]> Fold1 <tibble [2 × 4]> <tibble [0 × 3]>
## 2 <split [94/47]> Fold2 <tibble [2 × 4]> <tibble [0 × 3]>
## 3 <split [94/47]> Fold3 <tibble [2 × 4]> <tibble [0 × 3]>

Model 2:

set.seed(456)

office_fit_rs2 <- office_wflow2 %>%
  fit_resamples(folds)

office_fit_rs2

## # Resampling results
## # 3-fold cross-validation 
## # A tibble: 3 × 4
##   splits          id    .metrics         .notes          
##   <list>          <chr> <list>           <list>          
## 1 <split [94/47]> Fold1 <tibble [2 × 4]> <tibble [0 × 3]>
## 2 <split [94/47]> Fold2 <tibble [2 × 4]> <tibble [0 × 3]>
## 3 <split [94/47]> Fold3 <tibble [2 × 4]> <tibble [0 × 3]>

Cross validation, now what?

• We’ve fit a bunch of models
• Now it’s time to use them to collect metrics (e.g., R-squared, RMSE) on each model and use them to evaluate model fit and how it varies across folds

Collect CV metrics

Model 1:

collect_metrics(office_fit_rs1)

## # A tibble: 2 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard   0.373     3  0.0324 Preprocessor1_Model1
## 2 rsq     standard   0.574     3  0.0614 Preprocessor1_Model1

Model 2:

collect_metrics(office_fit_rs1)

## # A tibble: 2 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard   0.373     3  0.0324 Preprocessor1_Model1
## 2 rsq     standard   0.574     3  0.0614 Preprocessor1_Model1

Deeper look into CV metrics

Model 1:

cv_metrics1 <- collect_metrics(office_fit_rs1, summarize = FALSE) 

cv_metrics1

## # A tibble: 6 × 5
##   id    .metric .estimator .estimate .config             
##   <chr> <chr>   <chr>          <dbl> <chr>               
## 1 Fold1 rmse    standard       0.320 Preprocessor1_Model1
## 2 Fold1 rsq     standard       0.687 Preprocessor1_Model1
## 3 Fold2 rmse    standard       0.368 Preprocessor1_Model1
## 4 Fold2 rsq     standard       0.476 Preprocessor1_Model1
## 5 Fold3 rmse    standard       0.432 Preprocessor1_Model1
## 6 Fold3 rsq     standard       0.558 Preprocessor1_Model1

Model 2:

cv_metrics2 <- collect_metrics(office_fit_rs2, summarize = FALSE) 

cv_metrics2

## # A tibble: 6 × 5
##   id    .metric .estimator .estimate .config             
##   <chr> <chr>   <chr>          <dbl> <chr>               
## 1 Fold1 rmse    standard       0.388 Preprocessor1_Model1
## 2 Fold1 rsq     standard       0.529 Preprocessor1_Model1
## 3 Fold2 rmse    standard       0.421 Preprocessor1_Model1
## 4 Fold2 rsq     standard       0.266 Preprocessor1_Model1
## 5 Fold3 rmse    standard       0.411 Preprocessor1_Model1
## 6 Fold3 rsq     standard       0.518 Preprocessor1_Model1

Better tabulation of CV metrics

Model 1:

Fold	RMSE	R-squared
Fold1	0.320	0.687
Fold2	0.368	0.476
Fold3	0.432	0.558

Model 2:

Fold	RMSE	R-squared
Fold1	0.388	0.529
Fold2	0.421	0.266
Fold3	0.411	0.518

How does RMSE compare to y?

Recall that RMSE is calculated in the original units of the response variable.

\[RMSE_{\mbox{training}} = \sqrt{\frac{\sum_{i = 1}^n (y_i - \hat{y}_i)^2}{n}}\]

The CV RMSE uses 2/3 of the observations to build the model (\(\hat{y}_i\)) and 1/3 of the observations to test against. In the equation below “i” is in the 1/3. Note that \(\hat{y}_{\tiny\mbox{2/3 of fold 1}, \normalsize i}\) indicates the \(i^{th}\) row has been predicted using the model built on 2/3^{rds} of the observations.

\[RMSE_{\mbox{fold 1}} = \sqrt{\frac{\sum_{i \in \tiny \mbox{1/3 fold 1}} \normalsize (y_i - \hat{y}_{\tiny\mbox{2/3 of fold 1}, \normalsize i})^2}{n/3}}\]

In comparing which model is better, the CV RMSE provides information on how well the model did predicting each 1/3 hold out sample. Indeed, the RMSE is the error (read: variability) that continues to exist even after the model is built.

We can compare the model RMSE to the original variability seen in the imbd_rating variable.

Model 1:

cv_metrics1 %>%
  filter(.metric == "rmse") %>%
  summarise(
    min = min(.estimate),
    max = max(.estimate),
    mean = mean(.estimate),
    sd = sd(.estimate)
  )

## # A tibble: 1 × 4
##     min   max  mean     sd
##   <dbl> <dbl> <dbl>  <dbl>
## 1 0.320 0.432 0.373 0.0562

Model 2:

cv_metrics2 %>%
  filter(.metric == "rmse") %>%
  summarise(
    min = min(.estimate),
    max = max(.estimate),
    mean = mean(.estimate),
    sd = sd(.estimate)
  )

## # A tibble: 1 × 4
##     min   max  mean     sd
##   <dbl> <dbl> <dbl>  <dbl>
## 1 0.388 0.421 0.407 0.0168

Training data IMDB score stats:

office_ratings %>%
  summarise(
    min = min(imdb_rating),
    max = max(imdb_rating),
    mean = mean(imdb_rating),
    sd = sd(imdb_rating)
  )

## # A tibble: 1 × 4
##     min   max  mean    sd
##   <dbl> <dbl> <dbl> <dbl>
## 1   6.7   9.7  8.26 0.538

The original variability (measured by standard deviation) of the ratings was 0.538. After running Model 1, the remaining variability (measured by RMSE averaged over the folds) is 0.466; after running Model 2, the remaining variability (measured by RMSE averaged over the folds) is 0.52.

Conclusions:

• It seems as though the linear model does reduce the variability in the response variable (though not by much).
• It seems as though the linear model which includes the season as a factor variable is a (slightly) better model than the one that uses season as numeric.

Cross validation jargon

• Referred to as v-fold or k-fold cross validation
• Also commonly abbreviated as CV

Cross validation, redux

• To illustrate how CV works, we used v = 3:

• Analysis sets are 2/3 of the training set

• Each assessment set is a distinct 1/3

• The final resampling estimate of performance averages each of the 3 replicates

• It was useful for illustrative purposes, but v = 3 is a poor choice in practice

• Values of v are most often 5 or 10; we generally prefer 10-fold cross-validation as a default

10.4 Final model assessment

Now that Model 1 has been chosen as the better model, the test data is finally brought in to measure how well Model 1 will predict data in the wild (not that there are any additional wild episodes of The Office, but…).

Model 1:

office_preds1 <- office_wflow1 %>%
  fit(data = office_train) %>%
  predict(office_test) %>%
  bind_cols(office_test %>% select(imdb_rating, title)) 

office_preds1 %>%
  rsq(truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rsq     standard       0.476

office_preds1 %>%
  rmse(truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       0.412

The \(R^2\) on the test data is 0.562 (56.2% of the variability in the imdb_rating of the test data is explained by the model from the training data). Additionally, the test RMSE is 0.415. As expected, the RMSE is lower for training than test; the \(R^2\) is higher for training than test.

10.5 Reflection Questions

1. What are the steps of the workflow / pipeline?
   
2. What are the types of feature engineering that can be done with the step_ functions?
3. What is the different between model building and model assessment?
4. In the examples, was cross validation used for model building or model assessment?

10.6 Ethics Considerations

1. Why is it important to use different parts of the dataset to do the two different tasks of model building and model assessment?
2. How does cross validation help to keep the model from overfitting the data at hand?

Additionally, consider the example given by Aaron Roth in a blog titled Algorithmic Unfairness Without Any Bias Baked In. I’ve written it up as a full example.

The take away is:

with two populations that have different feature distributions, learning a single classifier (that is prohibited from discriminating based on population) will fit the bigger of the two populations

• depending on the nature of the distribution difference, it can be either to the benefit or the detriment of the minority population

• no explicit human bias, either on the part of the algorithm designer or the data gathering process

• the problem is exacerbated if we artificially force the algorithm to be group blind

• well intentioned “fairness” regulations prohibiting decision makers form taking sensitive attributes into account can actually make things less fair and less accurate at the same time

10.7 R: Full pipeline with CV + assessment

Using the same example as above, the process has been synthesized into the essential aspects / code.

10.7.1 The data

Break the data into test and training sets.

set.seed(123)
office_split <- initial_split(office_ratings) # prop = 3/4 by default
office_train <- training(office_split)
office_test  <- testing(office_split)

10.7.2 The model / enigne

Tell the computer to run linear regression using the lm() function.

office_spec <- linear_reg() %>%
  set_engine("lm")

10.7.3 The recipe(s)

Set the variables of interest (in the formula) and perform any necessary feature engineering.

office_rec1 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "id") %>%
  step_rm(air_date) %>%
  step_num2factor(season, levels = as.character(1:9)) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

office_rec2 <- recipe(imdb_rating ~ ., data = office_train) %>%
  update_role(title, new_role = "id") %>%
  step_rm(air_date) %>%
  step_dummy(all_nominal_predictors()) %>%
  step_zv(all_predictors())

10.7.4 The workflow(s)

office_wflow1 <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec1)

office_wflow2 <- workflow() %>%
  add_model(office_spec) %>%
  add_recipe(office_rec2)

10.7.5 Choice: fit the model? cross validate to decide between models?

Fit the model

office_fit <- office_wflow %>%
  fit(data = office_train)

The fit object is the same as the output of lm() that you are used to working with:

office_fit %>% tidy()

## # A tibble: 21 × 5
##    term         estimate std.error statistic  p.value
##    <chr>           <dbl>     <dbl>     <dbl>    <dbl>
##  1 (Intercept)  6.40     0.510        12.5   1.51e-23
##  2 episode     -0.00393  0.0171       -0.230 8.18e- 1
##  3 total_votes  0.000375 0.0000414     9.07  2.75e-15
##  4 season_X2    0.811    0.327         2.48  1.44e- 2
##  5 season_X3    1.04     0.343         3.04  2.91e- 3
##  6 season_X4    1.09     0.295         3.70  3.32e- 4
##  7 season_X5    1.08     0.348         3.11  2.34e- 3
##  8 season_X6    1.00     0.367         2.74  7.18e- 3
##  9 season_X7    1.02     0.352         2.89  4.52e- 3
## 10 season_X8    0.497    0.348         1.43  1.55e- 1
## # … with 11 more rows

office_fit %>% glance()

## # A tibble: 1 × 12
##   r.squared adj.r.squa…¹ sigma stati…²  p.value    df logLik   AIC   BIC devia…³
##       <dbl>        <dbl> <dbl>   <dbl>    <dbl> <dbl>  <dbl> <dbl> <dbl>   <dbl>
## 1     0.670        0.615 0.327    12.2 2.10e-20    20  -31.2  106.  171.    12.9
## # … with 2 more variables: df.residual <int>, nobs <int>, and abbreviated
## #   variable names ¹​adj.r.squared, ²​statistic, ³​deviance

Cross validate to choose between models

If cross validating, the model needs to be fit separately on each one of the hold out folds of the CV model. Here, v=5 is used, different from above where v=3 was used to simplify the explanation. Typically, the number of folds is 5 or 10.

Note that the objects are now similar to what you’ve worked with previously (output of lm()), but they contain a separate fit (i.e., linear model) for each of the CV folds.

set.seed(47)
folds <- vfold_cv(office_train, v = 5)

office_fit_rs1 <- office_wflow1 %>%
  fit_resamples(folds)

office_fit_rs2 <- office_wflow2 %>%
  fit_resamples(folds)

10.7.6 Assess the fit

On the test data

Note that we’d only assess the fit to the test data if we are done with the model building process and we’ve chosen the model we want to move forward with.

Again, \(R^2\) and RMSE are both calculated in a general sense (i.e., RMSE uses \(n\) in the denominator, not \(n-p\), I agree, it is confusing!).

If the first few lines don’t make sense, run the pieces. That is, run predict(office_fit, office_test) and then run office_test %>% select(imdb_rating, title) and then think about what it would mean to bind those columns together.

office_test_pred <- predict(office_fit, office_test) %>%
  bind_cols(office_test %>% select(imdb_rating, title))

rsq(office_test_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rsq     standard       0.468

rmse(office_test_pred, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       0.411

On the CV folds

Note the difference in the information. If you want the values per fold, don’t summarize. If you want the overall information, do summarize.

office_fit_rs1 %>% collect_metrics()

## # A tibble: 2 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard   0.355     5  0.0133 Preprocessor1_Model1
## 2 rsq     standard   0.579     5  0.0338 Preprocessor1_Model1

office_fit_rs2 %>% collect_metrics()

## # A tibble: 2 × 6
##   .metric .estimator  mean     n std_err .config             
##   <chr>   <chr>      <dbl> <int>   <dbl> <chr>               
## 1 rmse    standard   0.392     5  0.0284 Preprocessor1_Model1
## 2 rsq     standard   0.500     5  0.0563 Preprocessor1_Model1

office_fit_rs1 %>% collect_metrics(summarize = FALSE)

## # A tibble: 10 × 5
##    id    .metric .estimator .estimate .config             
##    <chr> <chr>   <chr>          <dbl> <chr>               
##  1 Fold1 rmse    standard       0.316 Preprocessor1_Model1
##  2 Fold1 rsq     standard       0.545 Preprocessor1_Model1
##  3 Fold2 rmse    standard       0.337 Preprocessor1_Model1
##  4 Fold2 rsq     standard       0.608 Preprocessor1_Model1
##  5 Fold3 rmse    standard       0.382 Preprocessor1_Model1
##  6 Fold3 rsq     standard       0.672 Preprocessor1_Model1
##  7 Fold4 rmse    standard       0.356 Preprocessor1_Model1
##  8 Fold4 rsq     standard       0.598 Preprocessor1_Model1
##  9 Fold5 rmse    standard       0.386 Preprocessor1_Model1
## 10 Fold5 rsq     standard       0.470 Preprocessor1_Model1

office_fit_rs2 %>% collect_metrics(summarize = FALSE)

## # A tibble: 10 × 5
##    id    .metric .estimator .estimate .config             
##    <chr> <chr>   <chr>          <dbl> <chr>               
##  1 Fold1 rmse    standard       0.307 Preprocessor1_Model1
##  2 Fold1 rsq     standard       0.607 Preprocessor1_Model1
##  3 Fold2 rmse    standard       0.357 Preprocessor1_Model1
##  4 Fold2 rsq     standard       0.572 Preprocessor1_Model1
##  5 Fold3 rmse    standard       0.458 Preprocessor1_Model1
##  6 Fold3 rsq     standard       0.471 Preprocessor1_Model1
##  7 Fold4 rmse    standard       0.387 Preprocessor1_Model1
##  8 Fold4 rsq     standard       0.555 Preprocessor1_Model1
##  9 Fold5 rmse    standard       0.450 Preprocessor1_Model1
## 10 Fold5 rsq     standard       0.293 Preprocessor1_Model1

Note that the variables in Model 1 perform better using cross validation than the variables in Model 2, we choose Model 1 to report out:

office_test_pred_1 <- office_wflow1 %>%
  fit(office_train) %>%
  predict(office_test) %>%
  bind_cols(office_test %>% select(imdb_rating, title))

rsq(office_test_pred_1, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rsq     standard       0.476

rmse(office_test_pred_1, truth = imdb_rating, estimate = .pred)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 rmse    standard       0.412